|
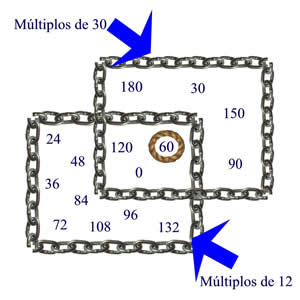
Mínimo Común Múltiplo El mínimo común múltiplo (m.c.m.) de dos o más números "es el múltiplo común a todos ellos, menor, distinto de cero". Ejemplo: Calcula el mínimo común múltiplo de los números 12 y 30.
Cálculo del Mínimo Común Múltiplo por descomposición factorial. Veamos el cálculo del mínimo común múltiplo de 12 y 30.
Luego el mínimo común múltiplo en descomposición factorial es: m.c.m. (12,30) = 22 x 3 x 5 = 60 Regla práctica: Para calcular el m.c.m. de dos o más números realizamos los siguientes pasos: 1.- Descomponer los números en factores primos. 2.- Coger todos los factores que aparecen en las descomposiciones. 3.- Colocar en dichos factores los exponentes mayores que hayan aparecido en las descomposiciones. Ejemplo.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
 Primer
paso: Escribimos los primeros múltiplos de ambos números.
Primer
paso: Escribimos los primeros múltiplos de ambos números.