|
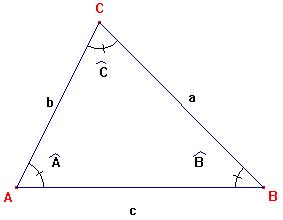
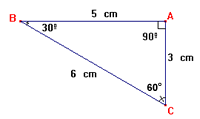
Un triángulo es un polígono de tres lados. Los tres lados de un triángulo determinan tres vértices, que los nombramos con letras mayúsculas (A, B, C). Los lados los designaremos con letras minúsculas (a, b, c). Asociado
a cada vértice tenemos un ángulo,
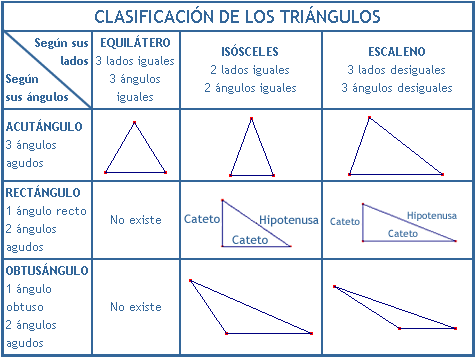
PROPIEDADES DE LOS TRIÁNGULOS
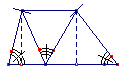
Primera Propiedad: “La suma de los tres ángulos de un triángulo es 180º ”. 1º. Dibuja un triángulo cualquiera y recórtalo.
2º. Pinta cada uno de los ángulos con un color distinto por las dos caras.
3º. Señala los puntos medios de dos lados.
4º. Dobla por la línea que une ambos puntos medios.
5º. Pliega por las líneas discontinuas los otros dos vértices.
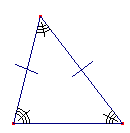
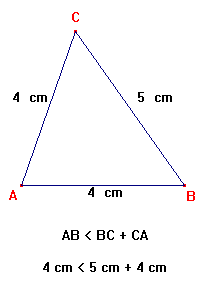
Segunda Propiedad: “En un triángulo, la longitud de un lado es menor que la suma de los otros dos”. 1º. Dibuja un triángulo ABC. 2º. Mide la longitud de sus tres lados. Observa que en todo triángulo, un lado es menor que la suma
de los otros dos.
IGUALDAD DE TRIÁNGULOS. Dos triángulos son iguales si tienen los tres lados y los tres
ángulos iguales.
PUNTOS Y RECTAS NOTABLES DE UN TRIÁNGULO. ALTURAS DE UN TRIÁNGULO Actividad Inicial Dibuja un triángulo en un folio. Traza una recta perpendicular desde cada vértice a su lado opuesto; dobla por esas rectas: el punto donde se cortan se llama Ortocentro. Observa la figura, te darás cuenta que la altura de un triángulo es la perpendicular que va desde el vértice hasta el lado opuesto.
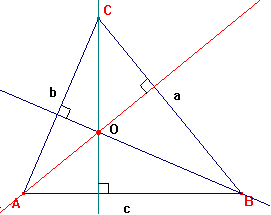
Vamos a trazar las tres alturas del siguiente triángulo.
Observa que las tres alturas se cortan en un punto (O), que llamamos ORTOCENTRO.
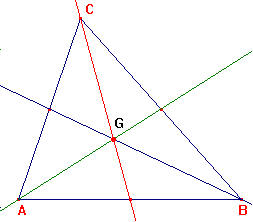
MEDIANAS DE UN TRIÁNGULO Actividad Inicial Dibuja un triángulo en un folio. Halla los puntos medios de sus tres lados. Recorta el triángulo con unas tijeras. Dobla desde cada uno de los vértices al punto medio del lado opuesto. Conseguirás con dobleces las medianas del triángulo, y con ellas el punto G, que es el baricentro.
Se llama MEDIANA de un triángulo a la recta que une un vértice con el punto medio del lado opuesto. Vamos a trazar las tres medianas del siguiente triángulo:
Observa que las tres medianas se cortan en un punto (G), llamado BARICENTRO.
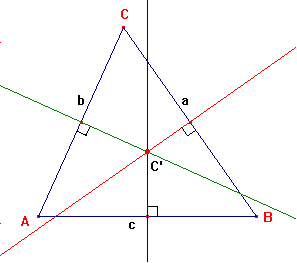
MEDIATRICES DE UN TRIÁNGULO Actividad Inicial Dibuja un triángulo en un folio. Halla los puntos medios de sus tres lados. Recorta el triángulo con unas tijeras. Dobla perpendicularmente desde cada uno de los puntos medios Conseguirás con dobleces las mediatrices del triángulo, y con ellas el punto C’, que es el circuncentro.
La mediatriz de un lado es la perpendicular al lado pasando por el punto medio. Vamos a trazar las tres mediatrices del siguiente triángulo.
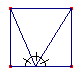
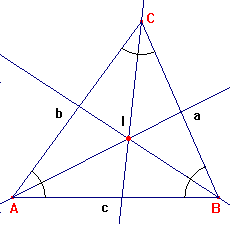
Observa que las tres mediatrices se cortan en un punto (C’), llamado CIRCUNCENTRO. BISECTRICES DE UN TRIÁNGULO. Actividad inicial. Dibuja un triángulo en un folio. Recorta con unas tijeras el triángulo. Obtén las bisectrices de los tres ángulos plegando el folio. Comprobarás que se cortan en un punto. La bisectriz de un ángulo es la semirrecta que divide al ángulo en dos partes iguales.
Vamos a trazar las bisectrices del siguiente triángulo.
Observa que las tres bisectrices se cortan en un punto (I), que llamamos INCENTRO. |