|
Medición de ángulos: Sistema Sexagesimal. |
| Primer ciclo de E.S.O. | |
| Introducción. | |
| Un ángulo
es la porción del plano comprendido entre dos semirectas
que tienen el mismo origen. Observa en la siguiente figura que dos semirectas con un origen común determinan siempre dos porciones del plano y por tanto dos ángulos, A y B. Al ángulo A se le llama ángulo convexo, mientras que el ángulo B es cóncavo.
Algunos ángulos especiales: Ángulo nulo, que es el ángulo definido por dos semirectas que coinciden. No barre ninguna porción del plano. Ángulo recto, que es el ángulo convexo definido por dos semirectas perpendiculares. Ángulo llano, cuando las dos semirectas que lo definen tienen la misma dirección, aunque sentidos opuestos. Barre un semiplano, esto es, la mitad del plano. Ángulo completo, que es el ángulo que abarca todo el plano. Los ángulos convexos siempre son menores que el ángulo llano. Los ángulos cóncavos por el contrario, son siempre mayores que el ángulo llano. Se llaman ángulos agudos a los que son menores que un ángulo recto. Se llaman ángulos obtusos a aquellos ángulos convexos (menores que un ángulo llano) que son mayores que un ángulo recto. |
| Medida de ángulos: el sistema sexagesimal. | ||
| Se llama grado sexagesimal, o simplemente grado (1º) a la medida del ángulo que resulta de dividir el ángulo recto en noventa partes iguales. Por tanto, el ángulo recto mide 90º. | ||
1. En este
ejercicio construye ángulos de 25º, 135º, 45º, 123º,
180º, 90º, 190º, 0º, 270º, 330º, 360º.
Apunta en tu cuaderno de qué tipo es cada uno de ellos.
|
||
| El transportador de ángulos. | |
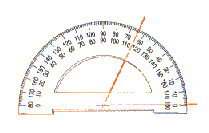 El
transportador de ángulos es una herramienta de dibujo
que nos permite medir y también construir ángulos. Consiste en un semicírculo graduado con el que podemos medir angulos convexos (hasta 180º) |
|
| En la siguiente escena arrastra el punto rojo de control y observa las medidas de los ángulos. | |
|
|
| 2. Construye con tu transportador los ángulos convexos del ejercicio anterior. Investiga cómo puedes construir ángulos cóncavos con el tranportador. | |
| Divisores del grado. | |
| Existen dos métodos para conseguir mayor precisión en la medida de un ángulo: el sistema decimal, que consiste simplemente en obtener decimales del grado, que es el método que utiliza el transportador de ángulos, o el sistema sexagesimal, que consiste en dividir el grado en 60 partes, en 60 minutos (60'); y cada minuto, en 60 segundos (60''). | |
| 3. En la
siguiente escena construye los siguientes ángulos y
anota en tu cuaderno si se trata de ángulos agudos u
obtusos: a. 56º 20' 40" b. 125º 15' 30" c. 18º 0' 0'' d. 18º 35' 10'' e. 18º 36' 0" |
|
|
|
| Observa que prácticamente no se aprecia diferencia entre los ángulos de los apartados c, d y e anteriores. Más adelante en otra lección estudiarás algún caso en el que será importante esa precisión. | |
 |
 |
 |
||||
 |
| Fernando Arias Fernández-Pérez | ||
 |
||
| © Ministerio de Educación y Ciencia. Año 2001 | ||
