Relaciones entre figuras geométricas en el plano

Lugares geométricos en el plano

Un lugar geométrico es un conjunto de puntos caracterizados por cumplir una misma propiedad. Así una circunferencia es el lugar de puntos del plano que están a igual distancia de otro llamado centro. La distancia común es el radio de la circunferencia.

 Lugar de un punto sobre un segmento que resbala apoyado en los lados de un ángulo recto

Intentemos presentar una situación real,  después hacer una interpretación geométrica ideal y resolver el problema matemáticamente.

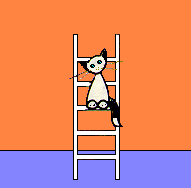Una escalera está situada sobre el suelo liso y apoyada con un extremo en la pared, se desliza hacia abajo. ¿Por qué línea se mueve el gatito sentado en el centro de la escalera?

Vista la escena de perfil, un tanto idealizada, tenemos un segmento (la escalera), los apoyos en la pared A y en el suelo B y la situación del gatito G.

Tras esta presentación realista, planteemos el siguiente problema matemático:

Sea un ángulo recto. Hallar el conjunto de centros de un segmento AB de una longitud dada d, cuyos extremos se hallan sobre los lados del ángulo dado. 

Trata de ver la solución e imagina la sucesión de puntos que ocupa G cuando la escalera se desliza (el punto A baja verticalmente y el punto B se desplaza horizontalmente hacia la derecha) ¿Qué trayectoria recorre G? 

¡A ver si has acertado!

EXPERIMENTA CON EL NIPPE DESCARTES...

El punto B es un control que permite hacer desplazamientos horizontales del mismo arrastrando con el puntero del ratón

El parámetro K es la razón en que el punto G, objeto del estudio, divide al segmento AB:  k =BG / GA. En nuestro caso, inicialmente toma valor k=1, puesto que al ser G el punto medio de AB se cumple que AG = GB.

Más adelante cambiando el valor de K, analizaremos otros lugares del punto G cuando el segmento AB desliza.

El ángulo recto lo hacemos coincidir con el primer cuadrante del plano cartesiano donde

 

El segmento AB tiene longitud 10

Desplaza el control B, comprobarás que el lugar del punto G es un cuadrante de circunferencia de radio OG.

1. ¿Cómo podemos explicar esto geométricamente?. Intenta dar una explicación observando la escena. Y finalmente consulta la solución  

2. Observa en la escena anterior que las coordenadas del punto G, x =ON e y =OM, son respectivamente la mitad de las distancias del origen O  a los puntos de apoyo B  y A, es decir x = OB/2 e y = OA/2. Intenta dar una explicación. Y finalmente consulta la solución.  .

Modifiquemos las condiciones iniciales del problema de la escalera y supongamos que el gatito no está sentado en medio de la escalera. Desde el punto de vista geométrico diremos que, ahora, la razón k = BG / GA no es 1, por ejemplo que BG = GA / 2, es decir K = 0.5

Un enunciado más general del problema es siguiente

Sea un ángulo recto. Hallar el lugar del punto G de un segmento AB que lo divide en dos partes desiguales, cuyos extremos se hallan sobre los lados del ángulo dado. 

Observemos los cambios:

  1. El lugar del punto  G cuando el segmento AB resbala no es una trayectoria circular

  2. La distancia OG no se mantiene constante a lo largo de la trayectoria.

  3. Las coordenadas del punto G no valen la mitad de OB y OA respectivamente (x distinto de OB/2, y distinto de OA/2)

  4. El punto G no es el corte de las diagonales del rectángulo AOBP

Habrás recordado la forma elíptica del lugar de puntos G.

Demostremos esta afirmación:

Si el segmento AB está inclinado un ángulo ß respecto al eje OB, entonces 

Elevando al cuadrado y sumando miembro a miembro

 

que es la ecuación de un elipse, centrada en el origen de semiejes a y b

Deslizando hacia la izquierda el punto B, lleva el segmento AB a la posición vertical, observa la posición que ocupa el punto G. Este punto (0,b) está en el eje de ordenadas a la altura más alta posible.

Desliza hacia la derecha el punto B, lleva el segmento AB a la posición horizontal, observa la posición que ocupa el punto G. Este punto (a,0) está en el eje de abcisas y ocupa la posición horizontal más alejada posible.

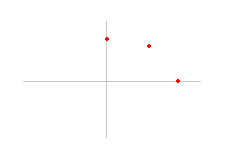Observa esta circunstancia en la figura adjunta, donde se representa una elipse centrada en el origen de semiejes a y b.  

 

Comprueba que ahora el lugar geométrico es una elipse pero ahora el semieje a es menor que el semieje b 

Se seguirá cumpliendo que   

 

Para concluir proponemos los siguientes problemas:

3. En realidad la ecuación de la elipse es válida incluso cuando los semiejes sean iguales a = b. Cuando esto ocurre hemos visto que el lugar es una circunferencia, centrada en el origen,  de radio r  = a = b.

Demuestra que la ecuación de la circunferencia es x2 + y2 = r2 

4. Una tablón de longitud 10 metros  está apoyado sobre una pared y un suelo liso y perpendicular a la pared. El punto de apoyo en el suelo dista de la pared 9 metro.

Una persona sube por el tablón. Calcula la altura a la que se encuentra dicha persona cuando:

        a) Ha andado 3 metros

        b) Ha andado 5 metros

        c) Ha recorrido todo el tablón.

Observa  el NIPPE, al ser la longitud del segmento AB=10, éste puede asimilarse al tablón del problema. Toma nota del resultado y trata de resolver el problema en tu cuaderno aplicando los conocimientos matemáticos 

SOLUCIONES

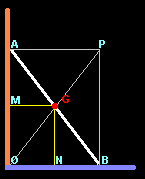
1. Para demostrar que el punto G describe un arco de circunferencia basta probar que la distancia de G al origen O es constante (radio de la circunferencia).

Empecemos por observar que el punto G es el punto medio del segmento AB, y AB representa una diagonal del rectángulo AOBP. La otra diagonal del rectángulo es OP. Como es propiedad de las diagonales de un rectángulo que se corten en su punto medio resulta que OG = GP = AG = GB = d/2, donde d es la longitud del segmento dado AB. 

Con lo que queda probado que la distancia OG es constante y vale d/2. volver

2. El triángulo OGB es isósceles puesto que, por lo visto en el problema anterior,  OG = GB =d/2. Por tanto la altura GN, es también mediana y el punto N es punto medio del segmento OB. Queda probado que x=ON  es la mitad de OB.

Análogamente, observando que el triángulo OGA es isósceles, se demuestra que y=OM es la mitad de OA. volver

3. Sustituyendo en la ecuación de la elipse a y b por r se obtiene como queríamos demostrar.

A este resultado se llega observando la relación que existe entre las coordenadas de un punto cualquiera de la circunferencia y el radio de la misma.

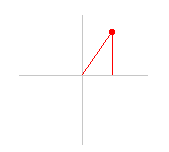En la figura adjunta se observa la formación del triángulo rectángulo, de catetos x e y e hipotenusa r. Aplicando el Teorema de Pitágoras se cumplirá x2 + y2 = r2 que representa la ecuación de la circunferencia centrada en el origen y radio r 

volver

4. Utilizando el NIPPE: 1º Pulsar inicio. 2º Deslizar el punto B hasta leer el valor OB = 9. 

a) Cuando ha andado 3 metros, la razón k = 3/7 = 0.43. Introduzcamos este valor y pulsamos limpiar.  Leeremos que la altura del punto es y=0.92. Solución: altura 92 cm 

b) Cuando ha andado 5 metros, está a mitad del recorrido total, la razón k=5/5=1. Introducimos este valor. Leemos que la altura del punto es y=2.17. Solución: altura 2.17 metros

c) Cuando ha recorrido todo el tablón alcanza la altura máxima, para OB= 9 metros podemos leer que OA = 4.35 Solución: 4.35 metros

volver

VOLVER A LA PÁGINA PRINCIPAL

 

Autor: ÁNGEL CABEZUDO BUENO

 
© Ministerio de Educación y Ciencia. Año 2000