Relaciones entre figuras geométricas en el plano

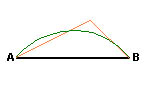
Fig. 1

• La recta es  más corta que cualquier otra línea que tenga los mismos extremos.

Distancia de un punto a una recta 

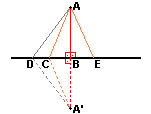
Fig. 2

• Menor longitud de los segmentos con origen en el punto y extremo en la recta: La tiene el segmento perpendicular.

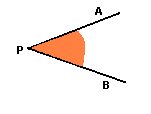
Fig. 3

• Vértice
• Lados
• Suma y resta de ángulos
• Producto y cociente de un ángulo por un número.

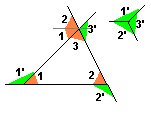
Fig. 4

• La suma de los ángulos interiores vale 180º
• La suma de los ángulos exteriores suma 360º
• La medida  ángulo exterior es igual a la suma de los dos interiores no adyacentes.

Mediatriz de un segmento. 

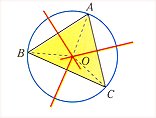
Fig. 5

• Recta perpendicular al segmento por el punto medio.
• Cada punto de la mediatriz equidista de los extremos del segmento.
• Las tres mediatrices de un triángulo se cortan en un punto llamado Circuncentro.
• El Circuncentro es el centro de la circunferencia circunscrita al triángulo.

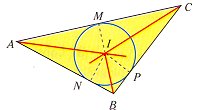
Fig. 6

• Recta que pasa por el vértice y lo divide en dos ángulos iguales.
• Cada punto de la bisectriz está a la misma distancia  de los lados del ángulo.
• Las tres bisectrices interiores de un triángulo se cortan en un punto llamado Incentro.
• El Incentro es el centro de la circunferencia inscrita al triángulo.

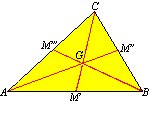
Fig. 7

• Segmento cuyos extremos son un vértice y el punto medio del lado opuesto.
• Las tres medianas se cortan en un mismo punto llamado Baricentro.
• La distancia del baricentro al vértice es el doble de la distancia del baricentro al punto medio del lado opuesto.

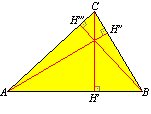
Fig. 8

• La altura de un triángulo es el menor segmento trazado desde un vértice al lado opuesto.
• La altura relativa a un lado es perpendicular a dicho lado trazada desde el vértice opuesto.
• Las alturas de un triángulo se cortan en un punto llamado Ortocentro

Circunferencia: arcos, cuerdas, ángulo central e inscrito, distancia de un punto a una circunferencia, recta tangente, posición relativa de dos circunferencias.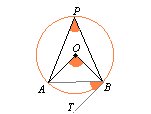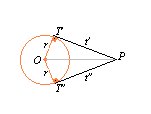

Fig.  9                                                           Fig.10

• Cada punto de la circunferencia dista lo mismo del centro. Cualquier segmento que une un punto cualquiera con el centro mide lo mismo y se llama radio.
• A arcos iguales les corresponden ángulos centrales iguales.
• Un ángulo inscrito mide la mitad del central que abarca el mismo arco. Fig 9. Como consecuencia un ángulo inscrito que abarca media circunferencia es recto. 
• La recta tangente a una circunferencia trazada por un punto exterior es perpendicular al radio correspondiente al punto de tangencia. Fig 10

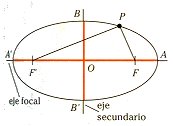
Fig. 11

• Lugar de puntos P tales que la suma de distancias  a otros dos puntos fijos F y F' (focos) es constante. PF+PF´=2·OA
• Una circunferencia es un caso particular de elipse, cuando F=F´= O. Entonces, OA= r y  PF+PF´=2·r
• Se dice que una circunferencia es una elipse de excentricidad cero ya que FF' = 0