
 |
RAZONES TRIGONOMÉTRICAS DE ÁNGULOS AGUDOS |
| Geometría | |
| 1. Razones trigonométricas en un triángulo rectángulo | ||
| Las razones trigonométricas de un
ángulo agudo se definen en función de los lados de ese triángulo y son independientes de su tamaño.
Las razones trigonométricas
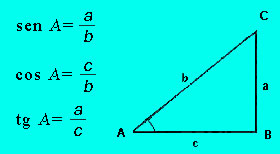
seno, coseno y tangente del ángulo agudo de un triángulo rectángulo como el de la figura, en el que el
ángulo B=90º, b es la hipotenusa, y a y c son los catetos, se definen:
Si se aumenta el tamaño de los lados del triángulo prolongándolos y trazando rectas paralelas al lado a se obtienen triángulos semejantes al anterior y, por tanto, las razones trigonométricas del ángulo A siguen siendo las mismas, dependiendo sólo de su amplitud (en grados o en radianes). Con Descartes vamos a poder comprobar esta propiedad. |
 |
|
| 1.- Varía los valores de b
hasta que alcance una longitud de 12.
2.- Observa cómo no varía el valor de las razones trigonométricas del ángulo de 30º que aparece en la figura. Cambia a 45º y 60º. 3.- Calcula las razones trigonométricas de los ángulos de 15º, 1 radián, 85º y 0.3 radianes.
4.-Intenta construir un triángulo rectángulo de lados 3, 4 y 5. ¿Qué valor toma el ángulo A? |
||
| 2.Un triángulo de hipotenusa unidad | ||
| Puesto que el valor de las razones trigonométricas en un triángulo rectángulo no dependen del tamaño de los lados, puede elegirse un triángulo cuya hipotenusa sea b=1. En este caso los cálculos se simplifican considerablemente, de forma que el cateto opuesto al ángulo es igual al seno y el contiguo al coseno. | ||
| 5.-
Repite en este caso el cálculo de las razones trigonométricas de los ángulos de 15º,
45º, 60º, 1 radián, 85º y 0.3 radianes.
6.- ¿Encuentras alguna relación entre las tres razones trigonométricas? Intenta escribir una fórmula que las relacione.
7.- Calcula el valor del ángulo A en los casos en que: sen A=0.5, cos A=0.75 y tg A=2.75 |
||
| Miguel García Reyes | ||
 |
||
| © Ministerio de Educación y Ciencia. Año 2001 | ||