COMPLEJOS números imaginarios

COMPLEJOS

NÚMEROS IMAGINARIOS

Existen ecuaciones que no tienen solución en el conjunto de los números reales, por ejemplo no tiene solución en R ya que no existe ningún número real que elevado al cuadrado dé -9. Para solucionar problemas en los que aparezcan raíces cuadradas de números negativos, es preciso ampliar el conjunto de los números reales R, construyendo un nuevo conjunto, C, de manera que R sea un subconjunto de C y de modo que en ese nuevo conjunto se conserven las propiedades de las operaciones y todos los números tengan raíz cuadrada. Para ello se define la unidad imaginaria.

Unidad imaginaria i, es aquel número que elevado al cuadrado da -1: ;

La ecuación tiene que cumplir , entonces:

La ecuación no tiene raíces reales ya que el discriminante es negativo.

NÚMEROS COMPLEJOS EN FORMA BINÓMICA

Una expresión de la forma a+bi en la que a y b son dos números reales cualesquiera e i es la unidad imaginaria, se denomina número complejo.
a+bi es la forma binómica del número complejo; a es la parte real y b es la parte imaginaria.

REPRESENTACIÓN GRÁFICA DE UN NÚMERO COMPLEJO

Cada complejo z = a+bi se representa por un vector con origen en el origen de coordenadas O, y extremo en el punto P(a, b). El punto P(a,b) se llama afijo del complejo.

a se representa sobre el eje de abscisas que recibe el nombre de eje real
b se representa sobre el eje de ordenadas que recibe el nombre de eje imaginario
Si b=0, el complejo a+bi se identifica con el número real a. Su afijo está sobre el eje real.
Si a=0, el número complejo a+bi tiene sólo parte imaginaria, recibe el nombre de imaginario puro. Su afijo está sobre el eje imaginario.
Si a=0 y b=0, el complejo a+bi es el complejo 0. Su afijo coincide con el origen de coordenadas.

1.- Representa en tu cuaderno los complejos:
z1=2; z2=3 i; z3=-1+ 5 i, z4=2- 4 i; z5=-3 -3 i; z6=4+3 i
Comprueba el resultado modificando los parámetros a y b en la escena anterior.

OPUESTO Y CONJUGADO DE UN COMPLEJO. REPRESENTACIÓN GRÁFICA.

Complejo: Complejo opuesto de z: Complejo conjugado de z:

a + bi - a - bi a - bi

2.- Halla los opuestos y conjugados de los complejos del ejercicio 1 y comprueba y observa su representación modificando los parámetros a y b en la escena anterior. Utiliza el cuaderno.

3.- Comprueba que se verifican las siguientes propiedades:

SUMA Y PRODUCTO DE COMPLEJOS EN FORMA BINÓMICA

Si z1= a + bi y z2 = c + di
su suma es: z1 + z2 =(a + bi)+(c + di)= (a+c)+(b+d)i
su producto es: z1·z2 =(a + bi)·(c + di)= (ac-bd)+(bc+ad)i
La diferencia z1-z2 = z1+(-z2)=(a + bi)+(-c - di) = (a-c)+(b-d)i

INVERSO DE UN NÚMERO COMPLEJO. COCIENTE DE NÚMEROS COMPLEJOS.

Si z = a+ bi siendo z ‡ 0, su inverso es: ,
se comprueba fácilmente que el producto de ambos es 1.
Si z1 = a + bi y z2 = c + di, siendo z2 ‡ 0, su cociente es:
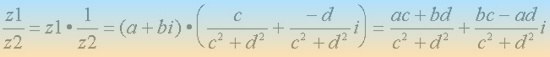
como

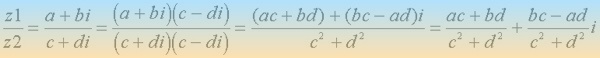
vemos que:

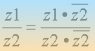
4.- Sean z1=4+3i, z2= -1+3i

Calcula en tu cuaderno: z1+z2; z1-z2; z1·z2;1/z2; z1/z2. Comprueba los resultados en la escena anterior, mirando los afijos de los complejos obtenidos.

POTENCIAS DE LA UNIDAD IMAGINARIA i

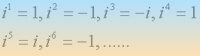
Teniendo en cuenta que , si queremos calcular, por ejemplo , dividimos 27 entre 4:
y vemos que: .
Luego la potencia de i con exponente "n" coincide con la potencia de i que tiene por exponente el resto de la división n entre 4.

5.- Calcula las potencias de i de exponentes: 25, 58, 243, -97, 164, -1545.
Observa cuál es su representación gráfica.

POTENCIA DE UN COMPLEJO EN FORMA BINÓMICA

Sea z = a+bi y n un número natural, teniendo en cuenta el desarrollo del binomio de Newton

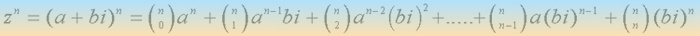
6.- Calcula en tu cuaderno y comprueba las siguientes potencias:

PRODUCTO DE UN NÚMERO COMPLEJO POR EL COMPLEJO i

Luego el vector que representa al complejo z·i se obtiene girando 90º en sentido positivo el vector que representa a z.

7.- Modifica los parámetros de la escena anterior y observa que el ángulo formado por los vectores que representan a z y z·i siempre es de 90º.

RAÍZ CUADRADA DE UN COMPLEJO EN FORMA BINÓMICA

La raíz cuadrada de un complejo z = a+bi es otro complejo x+yi tal que:

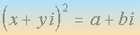
Resolviendo el sistema, obtenemos x e y.

8.- Calcula en tu cuaderno las raíces cuadradas de: 3+4i, -4+3i y 8-6i.

Comprueba los resultados utilizando la escena anterior.

Ir a forma polar
Ir a índice

Autor: Mª Ángeles Alonso González


	© Ministerio de Educación y Ciencia. Año 2001

Complejo:	Complejo opuesto de z:	Complejo conjugado de z:
a + bi	- a - bi	a - bi