
INECUACIONES DE 2º GRADO
Una inecuación de 2º grado es una expresión algebraica en la que interviene un polinomio de 2º grado y una de las cuatro desigualdades. Realizando operaciones y teniendo en cuenta las transformaciones válidas en una desigualdad podemos expresar cualquier inecuación de 2º grado en una expresión del tipo:
![]()
Las soluciones de la inecuación son todos los números reales "x" que verifican la desigualdad. Comprueba con la siguiente escena que una inecuación puede tener desde ninguna hasta infinitas soluciones:
1. Resuelve las siguientes inecuaciones utilizando la escena anterior, anota el resultado en tu cuaderno.
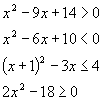
Las soluciones de una inecuación de 2º grado son generalmente un intervalo o la unión de dos intervalos de la recta real, los extremos de esos intervalos son precisamente las raíces del polinomio asociado a la inecuación. (Si el polinomio no tiene raíces reales estaremos ante un caso especial que estudiaremos más tarde)
Recuerda que si el polinomio de 2º grado tiene como raíces x1 y x2, lo podemos expresar de la siguiente forma: a(x-x1)(x-x2), donde "a" es el coeficiente líder del polinomio.
2. Resuelve las inecuaciones anteriores factorizando previamente el polinomio asociado. Utiliza la escena para comprobar la solución.
3. Escribe una inecuación que tenga como solución:
Si representamos la parábola asociada a la inecuación, parábola soporte, podemos comprobar que la solución de la inecuación corresponde con el conjunto de números reales donde la parábola queda por encima del eje OX.
4.- Haciendo uso de esta escena, resuelve las siguientes inecuaciones representando previamente la parábola soporte de cada una de ellas en tu cuaderno:
5.- ¿Una inecuación de segundo grado puede tener una única solución? Razona la respuesta y pon un ejemplo.
Si la parábola queda totalmente por encima o por debajo del eje OX (no corta al eje), el conjunto de soluciones de la inecuación puede ser todos los números reales o el conjunto vacío. Comprueba estos casos en la escena.
6. Escribe una inecuación de segundo grado que tenga por solución cualquier número real y otra que no tenga solución. Representa las parábolas correspondientes.
|
|||||||||||||||