

NÚMEROS COMPLEJOS
OPERACIONES EN FORMA POLAR
5. Multiplicación
Para multiplicar dos números complejos en forma polar se multiplican los módulos y se suman los argumentos
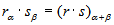
Ejemplo
El producto de
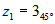 y
y 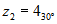 es
es
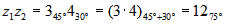 .
.
5.-
Comprobar que el producto de 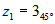 y
y
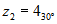 es
es 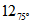 .
Observar gráficamente que al multiplicar dos números complejos en forma polar,
los módulos se multiplican y los argumentos se suman.
.
Observar gráficamente que al multiplicar dos números complejos en forma polar,
los módulos se multiplican y los argumentos se suman.
6. División
Para dividir dos números complejos en forma polar, se dividen los módulos y se restan los argumentos.
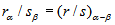
Ejemplo
El cociente de
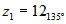 y
y
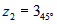 es
es 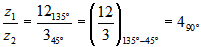 .
.
6.-
Comprobar gráficamente que el de
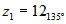 y
y 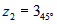 es
es 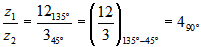 .
Observar gráficamente que al dividir dos números complejos en forma polar, los
módulos de dividen y los argumentos se restan.
.
Observar gráficamente que al dividir dos números complejos en forma polar, los
módulos de dividen y los argumentos se restan.
7. Potencia
Para elevar a una potencia un número complejo en forma polar se eleva el módulo al exponente y se multiplica el argumento por el exponente.
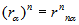
Ejemplo
La cuarta potencia de
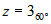 es
es 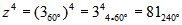 .
.
7.-
Comprobar que la cuarta potencia de 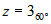 es
es
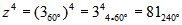 . Observar gráficamente que al eleva un
número complejo en forma polar a una potencia, se eleva el módulo a dicha
potencia y se multiplica el módulo por dicha potencia.
. Observar gráficamente que al eleva un
número complejo en forma polar a una potencia, se eleva el módulo a dicha
potencia y se multiplica el módulo por dicha potencia.
Fórmula de Moivre
La fórmula de Moivre es la potencia de un número complejo escrita en forma trigonométrica.
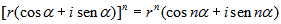
8. Radicación
Para hallar las raíces enésimas de un número complejo se hace la raíz enésima del módulo y se divide el argumento entre el índice. Un número complejo distinto de cero tiene tantas raíces complejas como indica el índice.
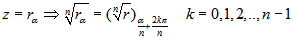
Ejemplo
Las cuatro raíces cuartas de 81
son 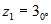 ,
,
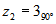 ,
, 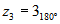 y
y
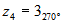 .
.
8.-
Comprobar que las
cuatro
raíces cuartas de 81 son 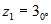 ,
,
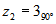 ,
, 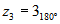 y
y
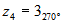 . Observar gráficamente que las raíces
enésimas de un número complejo forman un polígono regular de n lados centrado en
el origen.
. Observar gráficamente que las raíces
enésimas de un número complejo forman un polígono regular de n lados centrado en
el origen.
|