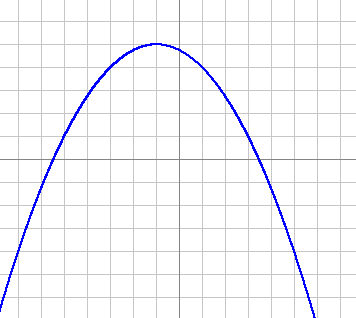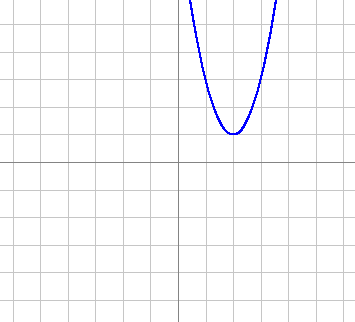
Considerando que en la actividad anterior concluimos que el vértice de la parábola y = a(x-b)2 + c es V = (b, c) y, como se aprecia en la gráfica, esta ubicación corresponde al punto (2,1), tenemos ya determinados los valores:
b = 2, c = 1.
Para encontrar el valor de a, debemos antes determinar otro punto por el cual pase la curva. En la gráfica puede verse que la parábola pasa por el punto (x, y) = (1,3). Sustituyendo en la ecuación los valores
x = 1, y = 3, b = 2, c = 1 se obtiene:
y = a(x-b)2 + c
3 = a(1-2)2 + 1
3 = a +1
a = 2
En consecuencia la ecuación de la parábola es:
y = 2(x - 2)2 + 1
Haga click sobre el dibujo para verificar lo obtenido.
Observación: ¿Qué hubiera sucedido si en lugar de seleccionar (1, 3) como punto de la parábola, hubiéramos escogido (3,3)?