
Las funciones hiperbólicas
La función Seno Hiperbólico: y=sinh(x) ó y=Sh(x)
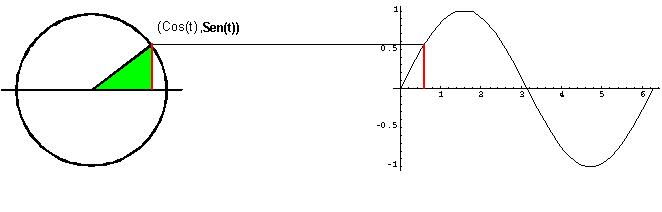
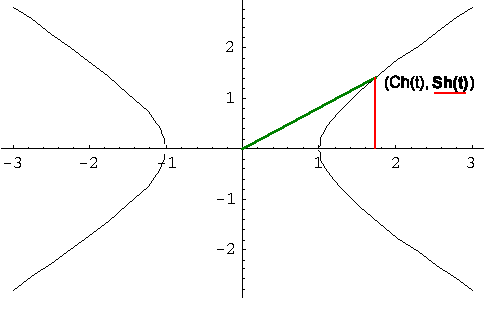
Si consideramos la hipérbola equilátera unitaria x2-y2=1, al intentar parametrizarla con funciones que simplifiquen sus derivadas, nos encontramos con unas funciones que nos recuerdan en muchos aspectos a las funciones trigonométricas circulares que se definían en la circunferencia goniométrica: x2+y2=1.
Así la funciones x=cos(t) y=sen(t) parametrizan la circunferencia unidad y sus derivadas satisfacen (cos(t))'= - sen(t); (sen(t))'=cos(t).

Ahora tenemos que las funciones: x=Ch(t)=(et + e-t)/2 y=Sh(t)=(et - e-t)/2 parametrizan la hipérbola equilátera x2-y2=1 y sus derivadas satisfacen (Ch(t))'=Sh(t); (Sh(t))'=Ch(t).
Apartado 1º
Nos proponemos analizar la función Seno hiperbólico, que se define como:
y=Sh(x)=(ex - e-x)/2
Actividades: Aprovechando la interactividad de la ventana anterior observa (desplazando el punto) cómo varía el Seno Hiperbólico al variar su variable independiente x. Modifica además, si lo necesitas, la escala y /o el posicionamiento de los ejes e intenta responder en tu cuaderno a las siguientes preguntas:
1)Rellena la siguiente tabla de valores
| x | -2 | __ | __ | __ | 2 |
| Sh(x) | __ | -1 | 0 | 1 | __ |
2)Hay algún tipo de simetría en la gráfica
3)¿El Sh(x) crece con x?
4)¿En qué momento el crecimiento es más lento?
Apartado 2º
Nos proponemos analizar la función Coseno hiperbólico, que se define como:
y=Ch(x)=(ex + e-x)/2
Actividades: Aprovechando la interactividad de la ventana anterior observa (desplazando el punto) cómo varía el Coseno Hiperbólico al variar su variable independiente x. Modifica además, si lo necesitas, la escala y /o el posicionamiento de los ejes e intenta responder en tu cuaderno a las siguientes preguntas:
1)Rellena, cuando sea posible, los valores que faltan en la siguiente tabla:
| x | -2 | __ | 0 | __ | 2 |
| Ch(x) | __ | -1 | __ | 1 | __ |
2)¿Hay algún tipo de simetría en la gráfica del Ch(x)?
3)¿Cuándo crece o decrece el Ch(x)?
4)¿En qué momento es mínimo el Ch(x)?
5)Ayudándote de la calculadora, verifica para algunos valores que aproximadamente:
Ch2(x) - Sh2(x)=1
rellena al respecto, la siguiente tabla:
| x | 2 | - 1 |
| Sh(x) | __ | __ |
| Ch(x) | __ | __ |
| Ch2(x) - Sh2(x) | __ | __ |
Apartado 3º
Nos proponemos analizar la función Tangente hiperbólica, que se define como:
y=Th=Sh(x)/Ch(x)=(ex - e-x)/(ex + e-x)
Actividades: Aprovechando la interactividad de la ventana anterior observa (desplazando el punto) cómo varía la Tangente Hiperbólica al variar su variable independiente x. Modifica además, si lo necesitas, la escala y /o el posicionamiento de los ejes e intenta responder en tu cuaderno a las siguientes preguntas:
1)Rellena, cuando sea posible, los valores que faltan en la siguiente tabla:
| x | -2 | __ | 0 | __ | 2 |
| Th(x) | __ | -0.5 | __ | 2 | __ |
2)¿Hay algún tipo de simetría en la gráfica de Th(x)?
3)¿Cuándo crece o decrece la Th(x)?
4)¿Puede sobrepasar la tangente hiperbólica el valor 1?. ¿Y bajar de -1?
Autor: Máximo Bolea Campo