
 |
APLICACIONES DE LA INTEGRAL DEFINIDA. CÁLCULO DE ÁREAS |
| 2º Bachillerato Ciencias Sociales | |
7)
Modifica los valores a y b,
según los valores de la tabla, y calcula en tu cuaderno el área.
(Observa como va afectando al número de recintos y a la expresión
de I)
8) Modificando los valores de f3, f2, f1, f0, a, b y repitiendo los pasos anteriores calcula en tu cuaderno el área limitada por la gráfica de la función f(x) = x3-4x2+3x y el eje X |
| 4.- CÁLCULO DEL ÁREA LIMITADA POR LA GRÁFICA DE DOS FUNCIONES. | |||
Para
calcular el área comprendida entre la gráfica de dos funciones
y
= f(x), y = g(x) se procede así
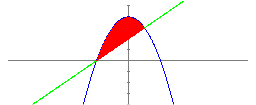 1. Calculamos la función diferencia y = (f-g)(x). |
|||
|
|||
| Anota
en tu cuaderno:
1) Cambia el valor de Paso = 1 para ver el área pedida. 2) Resuelve la ecuación f(x)-g(x) = 0. 3) Ordena de menor a mayor las soluciones obtenidas. (Paso = 2). 4) Calcula una primitiva G(x) de f(x)-g(x) (Paso = 3). 5) Calcula el valor de G(x) en cada una de las soluciones de f(x)-g(x) = 0. (Paso = 4). 6) El área pedida es la suma de las áreas de cada recinto. Y la de estos el valor absoluto de las diferencias de G(x). (Paso = 5). 7) Repitiendo los pasos anteriores calcula en tu cuaderno el área limitada por las gráficas de las funciones f(x) = x2+x-2 y g(x) = 2x |
|||
| Mª Dolores Chávez Gordito | ||
 |
||
| © Ministerio de Educación y Ciencia. Año 2003 | ||