
INTEGRAL DEFINIDA
Autor : Óscar Blasco Laín
I) Interpretación geométrica
Sea y=f(x) la gráfica de una función continua y positiva en el intervalo cerrado I=[a,b],con lo que podemos asegurar que es integrable según Riemann (ver apartado III). La interpretación geométrica de la integral definida de la función f(x) en el intervalo [a,b]
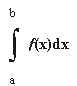
representa el área de la región de plano comprendida entre la gráfica de la función f(x), el eje de abscisas y=0 y las rectas x=a y x=b.
1.- Modifica los valores de a y b y observa la modificación progresiva del área resaltada. (Nota: utiliza los valores de escala y ejes si fuera necesario en la visualización completa).
2.- ¿Qué ocurre en la gráfica si coinciden los valores de a y b?. Relaciónalo con el valor calculado de la integral definida.
II) Cálculo aproximado del área limitada por una curva y el eje de abscisas
Sea y=f(x)=x^2+1 una función definida y positiva en el intervalo cerrado I=[0,2], siendo 14/3 el valor de la integral definida de f(x) desde x=0 hasta x=2.
Vamos a tomar un valor cualquiera del intervalo t1. Una aproximación del área comprendida entre la gráfica de la función f(x), el eje de abscisas y las rectas x=0 y x=2, sería el área del rectángulo cuya base es la longitud del intervalo, y la altura el valor de la función para el valor seleccionado:
S = f(t1)*(2-0)
La parte sombreada de color turquesa representa la parte del área del rectángulo que no se incluye en el valor de la integral, mientras que la sombreada en color gris es la que no se incluye en el área del rectángulo y sí está incluida en el valor de la integral.
3.- Modifica el valor seleccionado en el intervalo (t1) y observa el valor aproximado calculado. ¿Cuál es el valor de t1 que permite obtener el valor exacto de la integral definida?
Ahora vamos a dividir el intervalo I=[0,2]en 2 partes, mediante el valor central: [0,1] y [1,2],seleccionando un valor de cada una de las partes, t1 y t2 respectivamente.
Ahora la aproximación del área comprendida entre la gráfica de la función f(x), el eje de abscisas y las rectas x=0 y x=2, sería la suma del área de los rectángulos cuya base es la longitud de cada parte del intervalo, y la altura el valor de la función para los valores seleccionados en cada parte:
S = f(t1)*(1-0) + f(t2)*(2-1)
La parte sombreada de color turquesa representa la parte del área de los rectángulos que no se incluye en el valor de la integral, mientras que la sombreada en color gris es la que no se incluye en el área de los rectángulos y si está incluida en el valor de la integral.
4.- Modifica los valores seleccionados en cada una de las partes del intervalo (t1 y t2) y observa el valor aproximado calculado. ¿Cuál es el valor en cada intervalo que aproxima más el área al valor real?
5.- Con la misma función y el mismo intervalo, calcula el valor aproximado que se obtiene si se divide dicho intervalo en 4 partes iguales. Compara los valores obtenidos con el valor real si se selecciona el punto central dentro de cada de una de las partes.
III) Integral definida según Riemman
Si hacemos tender a infinito el número de partes del intervalo, y a la vez las longitudes de cada intervalo tienden a cero y la suma S no depende de los valores ti elegidos en cada intervalo, diremos que f(x) es integrable según Riemann en [a,b].Al límite al que tienden todas las sumas se le llama integral definida de la función f(x) en el intervalo [a,b] y se escribe :
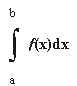
Se puede demostrar que toda función f(x) que sea continua en [a,b] es integrable según Riemann en [a,b].
IV) Aplicación de las integrales al cálculo de áreas
Vamos a calcular el área del triángulo de vértices A(1,2) , B(4,8) y C(5,6). Para ello, lo primero que hay que hacer es obtener las ecuaciones de los lados del triángulo.
Para calcular el área de la región comprendida entre las gráficas de dos funciones f(x) y g(x), tales que la primera va por encima de la segunda, en el intervalo [a,b]:
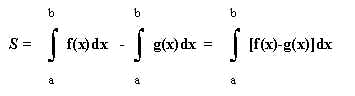
6.- Calcula el área del triángulo.(Solución S = 6 unidades de superficie).
Los contenidos teóricos de esta página se han obtenido del siguiente libro:
| PREPARANDO LAS PRUEBAS DE ACCESO A LA UNIVERSIDAD |
| Matemáticas Aplicadas a las Ciencias Sociales II |
| Alberto Atarés Gárate |
| Libreria General - Zaragoza - 1999 |