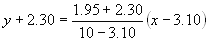EL MÉTODO DE LA SECANTE.
Consideremos la curva y=f(x), y la recta que pasa por los puntos A(a,f(a)) y B(b,f(b)). Si la función continua y=f(x) es tal que f(x)=0 posee una única raíz a en el intervalo (a,b), y f(a) y f(b) tienen signos opuestos, la cuerda AB cortará al eje OX en un punto X1 del intervalo (a,b), que junto con A ó B formará el nuevo intervalo (a1,b1).
El método de la secante consiste en ir aproximando el valor de la raíz buscada a mediante las sucesivas intersecciones con el eje OX de la cuerda que une dos puntos cuyas ordenadas son de signos distintos.
|
1.- PRIMERA
ITERACIÓN.
|
|||||||||||||||||||||||||||||
|
Partimos pues de los puntos A(a,f(a)) y B(b,f(b)). Llamamos a0=a, b0=b, y sea la recta que pasa por A y B la que tienes en la escena. Cuando esta recta corta al eje OX, tenemos la primera aproximación a la raíz buscada a, en nuestro caso inicial la recta es:
y al intersecar con el eje OX (recuerda OX: y=0) obtenemos el punto X1=6.83. A continuación calculamos f(X1).f(a0), f(X1).f(b0), y según nos salgan los signos, nos quedamos con aquel extremo cuya ordenada tenga distinto signo que f(X1) para la siguiente iteración. EN LA ESCENA En el PASO 0 puedes visualizar los puntos escogidos A0=A y B0=B, cuyas abcisas forman el intervalo [a,b]; el PASO 1 calcula la recta secante que une estos puntos; el PASO 2 interseca la secante con el eje OX, obteniendo X1; y el PASO 3 sitúa el punto sobre la gráfica de f(x), (X1,f(X1)).
|
|||||||||||||||||||||||||||||
|
2.- SEGUNDA ITERACIÓN.
|
|||||||||||||||||||||||||||||
|
En esta segunda iteración partimos de los puntos A1=A0 y B1=X1, que forman nuestro nuevo intervalo. Calculamos la recta que pasa por estos puntos A1 y B1 y nuevamente la intersecamos con el eje OX. Obtenemos así una nueva aproximación a la raíz buscada. Asignamos a este punto el valor X2 y calculamos f(X2). Multiplicamos este valor por f(A1) y por f(B1) pasa saber, igual que antes, con cuál de ellos nos quedaremos para la siguiente iteración. EN LA ESCENA En el PASO 0 verás los nuevos puntos que conforman el intervalo que contiene a la raíz; en el PASO 1 se traza la recta secante que une los puntos A1 y B1; en el PASO 2 se interseca con el eje de abcisas obteniendo X2 y en el PASO 3 ves el punto sobre la gráfica de f(x), (X2,f(X2)).
|
|||||||||||||||||||||||||||||
|
3.- TERCERA ITERACIÓN.
|
|||||||||||||||||||||||||||||
|
Para esta iteración partimos de los puntos A2=A1 y B2=X2, pues se verificaba que f(A1).f(X2)<0. Calculamos nuevamente la recta secante que los une, intersecamos con el eje de abcisas y llevamos el punto a la gráfica de f(x). EN LA ESCENA En el PASO 0 verás los nuevos puntos que conforman el intervalo que contiene a la raíz; en el PASO 1 se traza la recta secante que une los puntos A2 y B2; en el PASO 2 se interseca con el eje de abcisas obteniendo X3 y en el PASO 3 ves el punto sobre la gráfica de f(x), (X3,f(X3)).
|
|||||||||||||||||||||||||||||
|
4.- TABULANDO LA INFORMACIÓN. A la vez que vamos iterando, podemos recoger los resultados en una tabla como la siguiente:
|
|||||||||||||||||||||||||||||
5.- EJERCICIOS.
1.- Ve anotando tus propios cálculos en tu cuaderno a medida que descubres el método.
2.- Cambia los puntos iniciales A0 y B0. Haz tú mism@ los nuevos cálculos, representando en tu cuaderno aproximadamente los resultados, al igual que ves en las escenas.
3.- Para la tabla anterior, sigue realizando iteraciones hasta que tengas un decimal de la raíz buscada, ¿cómo sabes que es así?
4.- Repite este método para la función f(x)=1-x-sen(x) en el intervalo [0,1].