APLICACIONES DE LA INTEGRAL AL CÁLCULO DE ÁREAS
1. ÁREA DEL RECINTO DONDE INTERVIENE UNA FUNCIÓN POSITIVA
Dada una función continua f y positiva en un intervalo [a,b], el área del recinto comprendido bajo la gráfica y=f(x) y limitado por el eje de abscisas, la recta x=a y la recta x=b, viene dada por 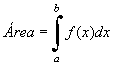area.gif (1200 bytes).
1.- Calcula el área del recinto limitado por la gráfica de la función problema1.gif (1057 bytes), el eje de abscisas y las rectas verticales x=-1 y x=2.
Modificando el valor de paso se puede observar las diferentes etapas para llegar a la solución.

2.- Calcula el área del recinto limitado por la función (x-2)ex y el eje de abscisas entre 2 y 3.

3.- Calcula el área del recinto limitado por la curva y=-x2, el eje de abscisas  y las rectas x=2 y x=4. ¿Qué ha ocurrido?.
2. ÁREA DEL RECINTO DONDE INTERVIENE UNA FUNCIÓN NEGATIVA
4.- Si la función f es negativa en un intervalo [a,b]. ¿De qué signo será la integral de f en ese intervalo?. Entonces, ¿el área puede ser igual a la integral?.

5.- Comprueba que las áreas de los recintos limitados por el eje de abscisas, las rectas x=a y x=b y las gráficas de las funciones f y -f son idénticas.

El control P (que se puede arrastrar) permite hacer un barrido por la gráfica de la función.

6.- Comprueba que las sumas de Riemman, tanto inferiores como superiores, de la integral de f y -f son opuestas. Deduce la relación que hay entre las integrales en un mismo intervalo de las funciones f y -f.
Los rectángulos rojo y turquesa se pueden mover arrastrándolos de sus respectivos controles. Son las aproximaciones por defecto y exceso respectivamente del recinto.
El parámetro n es el número de subintervalos de la partición y por tanto, condiciona el tamaño de la base de los rectángulos.
Dada una función continua f y negativa en un intervalo [a,b], el área del recinto comprendido encima de la gráfica y=f(x) y limitado por el eje de abscisas, la recta x=a y la recta x=b, viene dada por 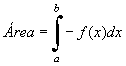areaneg.gif (1211 bytes).
3. ÁREA DEL RECINTO LIMITADO POR UNA FUNCIÓN ARBITRARIA
Dado que trabajamos con funciones continuas, aplicando el Teorema de Bolzano sabemos que en un intervalo o bien la función es positiva o bien negativa o bien si hay un valor de x donde es positiva y otro valor donde es negativa existirá un valor intermedio donde se hace cero.

7.- Calcula el área del recinto limitado por la gráfica de la función
f(x)=0.075(x+2)3-0.5(x+2)2-0.025x+1 las rectas x=-3, x=5 y el eje de abscisas. Indicación: los puntos de corte de la gráfica con el eje de abscisas entre -3 y 5 son x1=-0.37 y x2=4.34.

Si cambias el valor del parámetro paso podrás comprobar el proceso y la solución.

8.- Calcula el área del recinto limitado por la gráfica de la función coseno y el eje de abscisas entre 0 y 2*p .

9.- ¿Cuánto valdrá la integral definida de una función impar en un intervalo [-a,a].
4. ÁREA DEL RECINTO LIMITADO POR DOS FUNCIONES
Sean dos funciones f y g. El objetivo es calcular el área del recinto que encierran las gráficas de ambas funciones y las rectas x=a y x=b

10.- Calcula la superficie del recinto limitado por las funciones
f(x)=x(x+1)(x-3)/10+3 y
g(x)=0.08*(x-0.75)2+1, entre a=-2 y b=4.

El parámetro paso te permite al avanzar comprobar la solución.

11.-Deduce una fórmula general para calcular el área del recinto limitado por dos funciones que verifican en [a,b] la relación g(x)<f(x).

12.-¿Qué ocurrirá si alguna de las dos o ambas no son positivas?.

Si el parámetro situación toma el valor 1, el control M te permite desplazar verticalmente las funciones f y g.
13.-Demuestra que en general, el área del recinto limitado por dos funciones f y g con g<f es igual a la integral definida entre a y b de la función diferencia f-g independientemente del signo de cualquiera de ellas.

14.-Replantéate la situación si las funciones f y g se cortan.
Enrique Martínez Arcos
© Ministerio de Educación y Ciencia. Año 2001