|
|
Pasos de la escena
1.-Variar el valor del
parámetro esc para ver lo que ocurre al multiplicar un determinante, o
área por un número.
2.-Clic en animar,
así vemos lo que ocurre al tomar el segundo vector multiplicado por el número
(esc) escogido.
3.-Clic en Inicio
y
volver a comenzar.
Se pueden variar los parámetros de la escena,
introduciendo nuevos valores, o haciendo clic y arrastrando en los extremos de
los vectores azul y marrón de la izquierda
|
|
En
la izquierda de la escena se representa la suma de los dos determinantes,
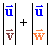 y en la derecha tenemos el area orientada definida por
y en la derecha tenemos el area orientada definida por
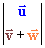
Si en la figura de la
izquierda intercambiamos el triángulo entre los segmentos marrones con el determinado por los 3 vectores marrones,
obtendremos la figura de la derecha.
Un clic en animar nos ayuda a verlo en este caso inicial. Es interesante ver
como en cualquier caso estas areas orientadas coinciden. En la escena, se pueden
variar los vectores fila haciendo clic en el extremo del
vector y arrastrándolo a una nueva posición; así observamos como las figuras de
la derecha y de la izquierda dan las mismas áreas orientadas.
Esta
propiedad y la anterior se resumen diciendo que el determinante de orden n es
multilineal
|
|
p4_
El determinante de la matriz identidad es gual a uno Esta
propiedad es evidente pues la matriz identidad
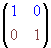 determina
un paralelogramo de base 1 y altura 1. determina
un paralelogramo de base 1 y altura 1.
|
Las
propiedades 2,3 y 4 caracterizan a los determinantes de orden n como
aplicación, del conjunto de las matrices cuadradas de orden n, en |R,
es decir, cualquier aplicación f: Mn(|R)
_____> |R que cumpla las
propiedades 2, 3 y 4 coincide con
el determinante: f(A)=detA.
El
determinante es la única aplicación de Mn(|R)
en |R que
cumple las
propiedades 2, 3 y 4
|
|
También
las propiedades 1, 2, 3a y 4 caracterizan a los determinantes de
orden n como aplicación, del conjunto de las matrices cuadradas de
orden n, en |R, es decir,
cualquier aplicación f: Mn(|R)
_____> |R que cumpla las
propiedades 1, 2, 3a y 4 coincide
con el determinante: f(A)=detA
El
determinante es la única aplicación de Mn(|R)
en |R que
cumple las
propiedades 1, 2, 3a y 4
|
|

