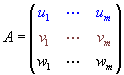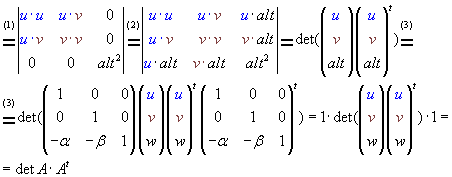Si u, v y w son los vectores fila pertenecientes a lR^m  de la matriz A,

el volumen al cuadrado del paralelepípedo que definen viene dado por

(área(u,v))².(altura)²=

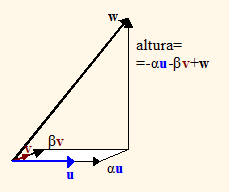
(1) El área definida por dos vectores es el elemento de volumen de la matriz cuyas filas son los dos vectores

(2) La altura es perpendicular a u y a v, por tanto u.alt=0 y v.alt=0

(3) Tenemos en cuenta que la altura es igual a -αu-βv+w

[Volumen del paralelepípedo definido por los tres vectores fila de la matriz A]=