DISTRIBUCIONES CONTINUAS
Estadística
 

Las distribuciones de probabilidad son idealizaciones de los polígonos de frecuencias. En el caso de una variable estadística continua consideramos el histograma de frecuencias relativas, y se comprueba que al aumentar el número de datos y el número de clases el histograma tiende a estabilizarse llegando a convertirse su perfil en la gráfica de una función. 

 

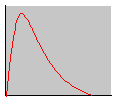
Las distribuciones de probabilidad de variable continua se definen mediante una función y=f(x) llamada función de probabilidad o función de densidad.

Así como en el histograma la frecuencia viene dada por el área, en la función de densidad la probabilidad viene dada por el área bajo la curva, por lo que:

1.Función de densidad y de distribución

2.Parámetros de una distribución

1. FUNCIÓN DE DENSIDAD Y FUNCIÓN DE DISTRIBUCIÓN

Llamaremos función de densidad de una variable aleatoria continua X a una función f que cumple:

  • es positiva

  • el área total bajo la curva, es decir entre f(x) y el eje de abscisas, es 1

  • el área determinada por f(x), el eje de abscisas y las rectas x=a, x=b, es la probabilidad de que la variable continua X esté en el intervalo [a,b], P(a£X£b)
1) Considera la función:

Comprueba que se trata de una función de densidad

En efecto f(x)³ 0 y el área total bajo la curva, en este caso un triángulo, es 1

 Si X es una variable aleatoria cuya función de densidad es f, calcula

  • p(X £ 0.75)=

  • p(X £ 1,25)=

  • p(0,75 £ X £ 1.25)=

Cambia el valor de a ó b, manteniendo a<b, y calcula el área

Como has visto en el ejercicio anterior la p(a£X£b) viene dada por el área entre la curva y=f(x) y el eje de abscisas desde a hasta b, si has estudiado ya cálculo integral sabrás que este área es:

p(a£X£b) = "área bajo la curva desde a hasta b" =

Dada una variable aleatoria X la función que asigna a cada número real la probabilidad p(X£x) se llama función de distribución. Viene dada por

2) La función de distribución correspondiente a la función de densidad anterior es

Observa que el área bajo la curva anterior de 0 a x, es la del triángulo de base x y altura 0,5x.

Calcula en la gráfica y compara los resultados con los obtenidos anteriormente

  • p(X £ 0.75)= F(0,75)=

  • p(X £ 1,25)= F(1,25)=

  • p(0,75 £ X £ 1.25)= F(1,25)-F(0,75)=

2. PARÁMETROS DE UNA DISTRIBUCIÓN DE PROBABILIDAD
Por analogía con las variables estadísticas podemos definir también aquí la media m y la desviación típica s de la variable aleatoria.

La media m, también llamada esperanza matemática, es un valor representativo de todos los valores que toma la variable aleatoria X, lo podemos imaginar como el punto sobre el eje de abscisas donde al poner una cuña la figura plana definida por la función de densidad quedará en equilibrio. Para calcularla hemos de hacer:

La desviación típica s es una medida de la dispersión de los valores que toma la variable aleatoria respecto de la media. Como ocurría con las variables estadísticas la desviación típica será más pequeña o más grande según la gráfica de la función de densidad sea más estrecha o más ancha en torno a la media. En este caso se calcula:
3) Comprueba, si sabes integrar, que en ejemplo anterior la media es 4/3 y la desviación típica 0,47
 

4) Considera la función de la escena:

Comprueba que se trata de una función de densidad

Calcula, mediante las áreas de las figuras correspondientes:

  • p(X £ 1,5)=

  • p(1,75 £ X £ 2,25)=

Por simetría, ¿cuál crees que es la media en este caso?

     
           
  María José García Cebrian
 
© Ministerio de Educación y Ciencia. Año 2001