La Distribución Binomial

B (n, p)

FUNCIONES DE PROBABILIDAD:

Llamamos función de probabilidad f a la aplicación de E(X) (Espacio Muestral) en el intervalo [0,1] que verifica:

f(A) = p(A)

Básicamente se trata de estudiar la probabilidad como una función utilizando para su estudio todas las propiedades de las funciones.

LA DISTRIBUCIÓN BINOMIAL:

Llamamos experiencia aleatoria dicotómica a aquella que sólo puede tener dos posibles resultados A y A'. Usualmente A recibe el nombre de éxito, además representaremos como p = p(A) y q = 1-p=p(A').

A la función de probabilidad de una variable aleatoria X resultado de contar el número de éxitos al repetir n veces una experiencia aleatoria dicotómica con probabilidad de éxito p la llamamos distribución binomial y la representamos por

B (n, p)

Para esta distribución se verifica que, la variable X puede tomar los valores:

0, 1, 2, ... , n

y que la variable toma cada uno de estos valores con probabilidad:

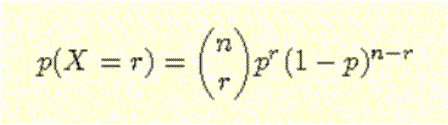
(deberás repasar las propiedades de los números combinatorios antes de continuar).

Ejercicio 1:

En la escena siguiente modifica los valores de n y de p para ver cómo se modifican las probabilidades de los distintos posibles valores de p (X=r)

(si se te superponen los decimales ve modificando el parámetro hasta que los veas con claridad)

Ejercicio 2:

Lanzamos 5 veces una moneda no trucada, ¿Cuál es la probabilidad de que obtengamos exactamente 2 caras?

(X = nº de caras en 5 lanzamientos. B (5, 0,5))

Comprueba el resultado obtenido con tu calculadora en la escena anterior haciendo n = 5 y p = 0,5 para el valor de r =2.

Ejercicio 3:

En un juego de azar la probabilidad de ganar una mano es 0,8. Calcula la probabilidad de que un jugador que juega 10 manos las gane todas y la probabilidad de que gane al menos 8.

Utiliza la escena de la actividad 1 para comprobar los resultados

Ejercicio 4:

Respondemos al azar a un test de 8 preguntas, cada una de las cuales tiene 4 opciones (solo una de ellas es verdadera). Para aprobar necesitamos contestar correctamente al menos a 6 de ellas. ¿Cuál es la probabilidad de aprobar?. ¿Y la probabilidad de fallar las 8?.

Utiliza la escena de la actividad 1 para comprobar los resultados.

PARÁMETROS DE UNA DISTRIBUCIÓN BINOMIAL:

Esperanza:

n · p

Desviación típica:

(n · p · q)^0.5 (raíz cuadrada)

AJUSTE DE UNA SERIE DE DATOS A UNA DISTRIBUCIÓN BINOMIAL:

Disponemos de una serie de k datos que toman los valores 0, 1, ... ,n.

Para saber si estos datos siguen pueden aproximarse por una distribución binomial:

1. Calculamos la media de los k datos y la igualamos a la Esperanza teórica de la Binomial (n · p). Despejamos de aquí el valor de p.
2. Calculamos los valores teóricos de p (X = r), multiplicándolos por k para obtener los valores teóricos de cada posible valor de la variable aleatoria en series de k datos.
3. Si la diferencia es "suficientemente pequeña" aceptamos como buena la aproximación Binomial, si no, la rechazamos.

(nota: la fundamentación estadística que nos permitiría decidir de manera objetiva si la diferencia entre los datos teóricos y los reales es "suficientemente pequeña" escapa de los objetivos de esta unidad didáctica, con lo cual la decisión se deberá tomar de manera subjetiva).

Ejercicio 5:

Lanzamos 5 chinchetas y observamos el número de ellas que caen con la punta hacia arriba.

Al repetir la experiencia 350 veces obtenemos:

¿Ajustan los resultados a una distribución Binomial? ¿Cuál sería el valor de p en caso afirmativo?

Comprueba el resultado obtenido con lápiz y papel con la siguiente escena. Cambia el valor de p y observa cómo varían los valores teóricos, intenta conseguir el ajuste óptimo y compruébalo con los resultados obtenidos aplicando el procedimiento descrito en este apartado.

Ejercicio 6:

Comprueba ahora si ajusta a una distribución binomial el número de CD's defectuosos encontrados en cajas de 3 unidades al abrir 100 de dichas cajas:

Autor: Pablo Antonio Martín Álvarez

	© Ministerio de Educación y Ciencia. Año 2001