
La campana de Gauss, curva de Gauss o curva normal, es una función de probabilidad continua, simétrica, cuyo máximo coincide con la media (m) y que tiene dos puntos de inflexión situados a ambos lados de la media, a una distancia (d) de ella.
Esta curva fue descrita por el matemático alemán Carl Friederich Gauss, estudiando los errores que se producen al medir reiteradamente una cierta magnitud.
La gran importancia de esta distribución se debe a la enorme frecuencia con la que aparece en las situaciones más variadas:
Caracteres morfológicos de individuos
Caracteres fisiológicos
Caracteres sociológicos
Caracteres físicos
Para cada valor de la media (m) y de la desviación típica (d) hay una curva normal, que se denomina N(m,d).
EJERCICIOS:
- Explica la influencia de la media (m) .
- Analiza las gráficas de la N(0,1), N(0,4), N(0,0.7) y explica la influencia de la desviación típica (d), en la dispersión de los datos.
Sin embargo, el reparto de probabilidades en ellas es prácticamente idéntico. Sólo depende de los parámetros m y d como veremos a continuación.
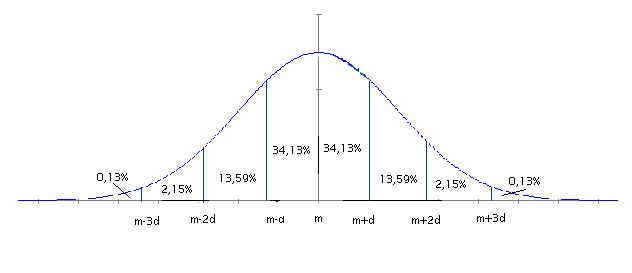
Por ser una distribución de probabilidad, el área bajo una curva normal cualquiera es 1 (100% de los casos). Esta área se distribuye, expresando la probabilidad en tantos por ciento del siguiente modo:
El 68,26% de las observaciones están comprendidos en el intervalo (m-d , m+d).
-Esto significa que si el cociente intelectual de las personas de un cierto colectivo es una N(112 ; 6), el 68,26% de ellos tiene un cociente intelectual entre 106 y 118..
El 95,44 % de las observaciones están comprendidos en el intervalo (m-2d , m+2d).
-Siguiendo con el ejemplo anterior el 95,44% de ellos tiene un cociente intelectual entre 100 y 124..
El 99,74 % de las observaciones están comprendidos en el intervalo (m-3d , m+3d).
-Siguiendo con el ejemplo anterior el 97,74% de ellos tiene un cociente intelectual entre 94 y 130.
Con los datos anteriores sobre el porcentaje de individuos y el hecho de que la curva sea simétrica, nos permite construir la siguiente distribución:
Ejercicio:
El cociente intelectual de los 3500 funcionarios de una provincia se distribuyen según una N(112,6). Calcular aproximadamente cuántos de ellos tienen: a) más de 112; b) entre 106 y 118; c) entre 106 y 112; d) menos de 100; e) más de 130; f) entre 118 y 124.
AAutor: Ángel Enríquez de Salamanca