
Correlación y regresión (Introducción).
Relación entre variables.
Muy a menudo se encuentra en la práctica que existe una relación entre dos (o más) variables. Por ejemplo: los pesos de los hombres adultos dependen en cierto modo de sus alturas; las longitudes de las circunferencias y las áreas de los círculos dependen del radio, y la presión de una masa de gas depende de su temperatura y de su volumen.
Si todos los valores de las variables cumplen exactamente una relación exacta, entonces se dice que las variables están perfectamente correlacionadas o que hay una correlación perfecta entre ellas o, más sencillamente, que existe una función o una fórmula que las relaciona.
Así la longitud L de una circunferencia y su radio r están perfectamente correlacionados pues se verifica exactamente que :
L = 2p r
Por el contrario, si se lanzan simultáneamente dos dados unas cuantas veces, no existirá una relación entre los puntos que se obtengan en cada dado (salvo que los dados estén cargados), es decir no existirá correlación entre las puntuaciones de cada dado.
En otros casos, parece que existe cierta correlación, aunque ésta no sea perfecta. Por ejemplo, las variables altura y peso de los individuos parecen tener cierto grado de relación aunque no exista una fórmula que nos permita adivinar el peso de un individuo conocida su altura.
Entonces, surge la siguiente pregunta fundamental:
¿En qué medida están relacionados la altura y el peso de un individuo?
Si somos capaces de encontrar una forma de medir adecuadamente esa relación, entonces, por ejemplo, podemos decidir si la altura y el peso de un individuo están mas relacionados entre sí que la altura de ese individuo y la altura de su padre.
Cuando se busca una medida para medir esa relación se dice que se está buscando medir la correlación entre esas dos variables.
Por tanto, averiguar la correlación entre dos variables se refiere siempre a hallar una medida de la relación entre esas dos variables.
Cuando se trata de dos variables solamente, se habla de correlación simple y cuando se trata de más de dos variables se habla de correlación múltiple.
Aquí vamos a tratar solamente de la correlación simple.
Volviendo al ejemplo de la altura y el peso de un individuo, y aunque todos aceptemos que no existe una fórmula exacta que relacione esas dos variables, sí que parece bastante difícil (aunque no totalmente imposible, en principio) que una persona de 120 kilogramos de peso mida 80 centímetros de altura.
Es decir, surge otra pregunta fundamental:
¿Podríamos hallar una fórmula para estimar -siquiera aproximadamente- el peso de un individuo a partir de su altura (o al revés)?
Cuando se busca una fórmula de ese tipo se dice que se está buscando una regresión entre esas dos variables.
Por tanto, hallar una regresión entre dos variables se refiere siempre a hallar una fórmula o ecuación que represente la relación aproximada entre esas dos variables.
Y de la misma forma que antes, cuando se trata de dos variables solamente, se habla de regresión simple. Cuando se trata de más de dos variables se habla de regresión múltiple.
Aquí vamos a tratar solamente de la regresión simple.
Correlación y regresión (I).
Nube de puntos.
Para estudiar y medir la relación entre dos variables, el primer paso es recoger los datos que muestren los correspondientes valores de las variables consideradas.
Por ejemplo, si disponemos de los datos de la altura y del peso de 100 individuos, lo primero sería representar en un gráfico cartesiano los 100 puntos (x,y) donde x e y serían la altura y el peso respectivo de cada individuo.
El conjunto de puntos que así se obtiene se suele denominar diagrama de dispersión o mas sencillamente nube de puntos.
Por ejemplo, en la escena siguiente se puede contemplar una nube de puntos real, obtenida a partir de datos reales de los que luego hablaremos.
Propuesta de trabajo:
Observarás que la nube de puntos está constituida por doce elementos, denominados con las doce primeras letras del alfabeto.
Si haces "clic" sobre cada punto verás que aparecen las coordenadas del mismo.
Si te apetece, puedes jugar con los otros botones y no te preocupes si te equivocas, pues siempre puedes volver a la situación inicial pulsando el botón denominado inicio.
De hecho, necesariamente deberás manejar esos botones para ver el punto L, que no se encuentra en la imagen inicial.
Tarea A) Lo que te pedimos, en primer lugar, es que escribas en un papel las coordenadas de cada uno de los doce puntos.
La primera coordenada corresponde al dato estadístico del llamado Índice de Precios Industriales (IPRI), elaborado por el Instituto Nacional de Estadística (INE) y que es un dato que pretende medir la evolución de los precios de los productos industriales.
La segunda coordenada corresponde al llamado IBEX-35 que es el índice de referencia mas importante de la Bolsa española. Para facilitar su representación en la escena anterior, los valores reales se han dividido por 100.
En la Bolsa de Nueva York, la aparición del IPRI americano tiene gran influencia, cosa que no ocurre (hasta ahora) en la Bolsa española.
Precisamente, lo que tratamos de estudiar es qué correlación existe entre ambas variables y si sería posible estimar el IBEX-35 a partir del IPRI.
Los datos que se han usado en los doce puntos corresponden a los doce últimos datos mensuales de ambas variables, disponibles el 1 de enero del año 2000.
Como dato mensual del IBEX-35 se ha usado el de cierre del primer día hábil en la Bolsa de cada uno de los doce meses de 1999.
Respecto al IPRI, el dato usado es el más reciente en cada uno de esos primeros días hábiles, es decir el que hipotéticamente puede haber influido más. Concretamente, los 12 datos del IPRI usados son los correspondientes a noviembre y diciembre de 1998 y los diez primeros meses de 1999.
Tarea B) En segundo lugar, lo que te pedimos es que estudies detenidamente la nube de puntos anterior y que intentes seleccionar aquellos puntos que te parecen mas "raros" o que se alejan mas del resto.
Correlación y regresión (II).
Recta de ajuste.
Con el diagrama de dispersión o nube de puntos, es posible frecuentemente representar una curva que se aproxime a los datos.
Tal curva se llama curva de aproximación.
En la mayor parte de las nubes de puntos obtenidas a partir de casos reales es difícil imaginarse cuál sería la mejor curva de aproximación y, generalmente, hay que optar por una determinada (usando algunos criterios específicos) que se suele denominar curva de ajuste.
Nosotros vamos a usar como criterio el de la simplicidad y dado que la curva mas sencilla es la recta, vamos a optar por buscar una recta de ajuste que se ajuste adecuadamente a nuestra nube de puntos.
Desde luego, la forma mas sencilla de obtener una recta de ajuste es dibujando una recta encima de la nube de puntos, tratando de que dicha recta se ajuste lo mejor posible a la nube de puntos.
Observa la escena siguiente y comprueba que puedes obtener otra recta moviendo el punto P y modificando la pendiente m. Para mover el punto P puedes arrastrarlo directamente con tu ratón, o bien usar los controles situados debajo de la escena y para modificar la pendiente m puedes usar el control de la pendiente situado también debajo de la escena y no olvides que siempre puedes volver a la posición inicial pulsando el botón inicio.
Propuesta de trabajo:
Lo que intentamos es encontrar gráficamente una buena recta de ajuste.
Tarea C) Lo que te pedimos ahora es que escojas aquella recta que, en tu opinión, se ajuste mejor a la nube de puntos.
Para ello, haz todas las pruebas que consideres necesarias y, cuando hayas escogido tu recta de ajuste, apunta el valor de la pendiente y las coordenadas del punto usado, de modo que puedas comparar posteriormente tu elección con la elección de los matemáticos.
Correlación y regresión (III).
Recta de regresión por mínimos cuadrados.
Es fácilmente comprensible que los matemáticos hayan intentado encontrar un procedimiento común para seleccionar la misma recta de ajuste, de modo que todo el mundo esté de acuerdo y no haya que atenerse a opiniones subjetivas.
La recta de ajuste seleccionada por los matemáticos es la llamada Recta de regresión por mínimos cuadrados y que se obtiene seleccionando de entre todas las rectas de ajuste posibles, aquélla que hace mínimo la suma de los cuadrados de las distancias verticales de los puntos a la recta (ahora te explicamos todo esto).
Propuesta de trabajo:
A partir de la escena anterior, puedes hacerte una idea de cómo los matemáticos han seleccionado su mejor recta de ajuste.
Lo que han hecho es seleccionar aquella recta que hace mínimo el resultado de sumar el cuadrado de cada una de las longitudes representadas en color magenta.
Esto se ha hecho así por diversas razones pero es importante precisar que podía haberse hecho de otra forma y que, incluso, en determinados casos especiales se prefiere usar otro criterio para la selección de la mejor recta de ajuste, aunque el caso aquí desarrollado es, desde luego, el más frecuente.
Ese cuadrado (de cada una de los segmentos de color magenta) se puede imaginar como el área de cada uno de los cuadrados que podrían construirse sobre cada uno de esos segmentos de color magenta.
Tarea D) Lo que te pedimos ahora es que escojas aquella otra recta que, en tu opinión, se ajuste mejor a la nube de puntos, usando el criterio de los matemáticos.
Para ello, haz todas las pruebas que consideres necesarias y, cuando hayas escogido tu recta de ajuste usando el criterio de los matemáticos, apunta el valor de la pendiente y las coordenadas del punto usado, de modo que puedas comparar posteriormente tu elección con el resultado correcto, calculado matemáticamente con toda exactitud.
Correlación y regresión (IV).
Ecuación de la recta de regresión por mínimos cuadrados.
A continuación vamos a indicar cuál es la ecuación de la recta de regresión por mínimos cuadrados, sin entrar en las demostraciones matemáticas exactas.
Para calcular la ecuación de la recta de regresión por mínimos cuadrados se hace lo siguiente, que explicamos paso a paso, indicando también las fórmulas exactas.
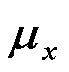 ) y la desviación
típica (
) y la desviación
típica ( Las fórmulas exactas para lo anterior son las que siguen.
Denotamos a los doce puntos de la nube de puntos de la siguiente forma:
(x![]() , y
, y![]() ) , (x
) , (x![]() , y
, y![]() ) , ... ,(x
) , ... ,(x![]() ,
Y
,
Y![]() )
)
Entonces, se tiene:
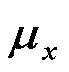 =
=
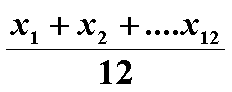
![]() =
=
![]() =
=![]()
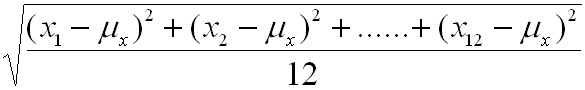
![]() =
= +
+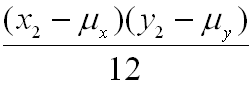 + . . . +
+ . . . +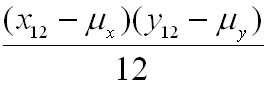
Hecho todo lo anterior, se obtiene la ecuación de la recta de regresión por mínimos cuadrados de la forma siguiente:
y - ![]() = m (x -
= m (x - ![]() )
)
donde la pendiente m es igual a:
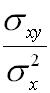
Es decir que la recta de regresión por mínimos cuadrados es la recta que pasa por el punto
(![]() ,
,![]() ) y que tiene por pendiente
a:
) y que tiene por pendiente
a: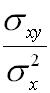
Y si aplicamos las fórmulas anteriores a nuestra nube de puntos (y redondeando para usar sólo tres decimales), resulta la recta siguiente, que es la la recta de regresión por mínimos cuadrados de nuestra nube de puntos:
y = 15,283 + 0,711x
En la siguiente escena, hemos representado en color magenta a dicha recta de regresión por mínimos cuadrados de nuestra nube de puntos y se trata de que la compares con tus rectas de ajuste obtenidas anteriormente, en las Tareas C y D anteriores.
Propuesta de trabajo:
Usando los controles inferiores de la escena, representa en ella a tus rectas de ajuste (seleccionadas en las tareas C y D anteriores) y compáralas con la recta matemáticamente obtenida y que figura representada en color magenta.
Tarea E) Lo que te pedimos ahora es que escribas un breve informe, tratando de explicar tus resultados en comparación a la recta de regresión por mínimos cuadrados y, especialmente, tratando de indicar si la recta de ajuste de los matemáticos te parece una buena opción, es decir si se ajusta bien a la nube de puntos (en tu opinión) o no y las razones de todo ello.
Correlación y regresión (V).
Coeficiente de correlación lineal.
A continuación vamos a hablar de la medida usual de correlación lineal
entre dos variables, el llamado Coeficiente de correlación lineal
( ![]() , léase "ro").
, léase "ro").
Hecho todo lo anterior, es muy fácil calcular dicho coeficiente, a partir de la fórmula siguiente:
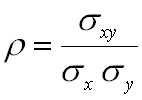
donde ![]() se define de forma análoga a
se define de forma análoga a ![]() , es decir:
, es decir:
![]() =
=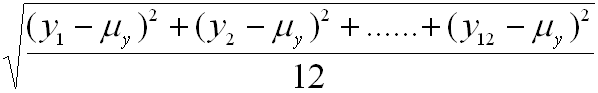
Lo que este coeficiente ![]() mide es el grado de ajuste de la recta de
regresión a una determinada nube de puntos.
mide es el grado de ajuste de la recta de
regresión a una determinada nube de puntos.
Cuanto mayor sea este ajuste, más confiados debemos estar en que es correcto usar a una recta como modelo de nuestra nube de puntos, pero si el ajuste no se considera bueno, deberemos pensar que nuestra nube de puntos no se representa bien por una recta y habrá que buscar otros modelos (quizás nuestra nube de puntos se ajuste mejor a una parábola, por ejemplo).
Conviene también destacar que a partir de la definición anterior, se puede comprobar que la ecuación de la recta de regresión puede expresarse también como:
y - ![]() = m(x -
= m(x - ![]() )
)
donde la pendiente m es igual a:

Es decir que la recta de regresión por mínimos cuadrados es la recta que pasa por el punto
(![]() ,
,![]() ) y que tiene por pendiente
:
) y que tiene por pendiente
:

Algunas consideraciones importantes sobre el coeficiente de correlación lineal:
-1 ![]()
![]()
![]() 1
1
¿Qué puede deducirse si se rechaza la existencia de correlación lineal si, por ejemplo, se encuentra un coeficiente de correlación lineal de 0,3 entre dos variables?
Propuesta de trabajo:
Usando la fórmula anterior y los datos obtenidos en la Tarea A vamos a hacer un ejercicio de cálculo del coeficiente de correlación lineal y otros dos de estudio de predicciones (a partir de los doce datos de la nube de puntos, obtenida con datos del IPRI y del IBEX-35).
Tarea E) Lo que te pedimos ahora es que calcules el coeficiente de correlación lineal entre el IPRI y el IBEX-35, a partir de los datos de la nube de puntos y, en función del resultado que obtengas, indiques si, en tu opinión, se puede decir o no que dichos IPRI e IBEX-35, están o no correlacionados linealmente.
Tarea F) Y ahora se trata de comparar los resultados del IBEX-35 con los que se obtienen a partir de la recta de regresión. Para ello, lo único que tienes que hacer es (en la ecuación que ya hemos calculado de la recta de regresión, es decir: y = 15,283 + 0,711x) sustituir la x por cada uno de los valores del IPRI y comparar el resultado que se obtiene con el correspondiente valor real del IBEX-35 y aconsejar sobre si vale la pena o no jugarse el dinero en la bolsa usando el IPRI como mecanismo de predicción.
Tarea G) A partir de los datos del IPRI (que son públicos y que se pueden obtener en el INE (en http://www.ine.es, por ejemplo), realiza tus propias predicciones del IBEX-35 en base a los datos del IPRI y compara luego los resultados obtenidos usando los datos del IBEX-35 publicados en cualquier periódico.
Correlación y regresión (VI).
Influencia de los valores extremos.
Bueno, probablemente puedas estar un poco decepcionado pues no parece que exista mucha correlación lineal entre las variables escogidas.
Lo que intentamos ahora es hacerte ver y reflexionar sobre la influencia de los valores extremos, un problema general a todos los procedimientos estadísticos o matemáticos basados en la media aritmética pues ocurre que un sólo valor puede arrastrar a toda la media aritmética detrás de sí.
Si has realizado la Tarea B anterior, habrás seleccionado ya algún valor aparentemente anómalo y muy probablemente habrás escogido como tal al punto L, que parece muy alejado del resto.
Pero hay que tener cuidado pues por muy anómalo que pueda parecer dicho punto L, corresponde absolutamente a un dato real y su alejamiento del resto de los puntos de la nube de puntos se debe a la fuerte subida del IBEX-35 a finales de 1999.
Volviendo a nuestro análisis sobre la influencia de los valores extremos, digamos que la media aritmética hace demasiado caso a los valores individuales, no debería dejarse influenciar tanto y ser mas resistente a ellos, mas robusta.
Para tu mayor tranquilidad, en esta última actividad no hay ninguna propuesta de trabajo ni ninguna tarea para realizar.
Sólo te pedimos que muevas el punto L de la escena siguiente y compruebes cómo sólo ese punto arrastra tras de sí a toda la recta de regresión.
En función de lo que vayas viendo, te sugerimos una serie de preguntas para reflexionar:
¿No ocurre que la recta de regresión es demasiado influenciable por un sólo valor?
¿Que puede ocurrir si un sólo valor es erróneo o anómalo?
¿No convendrá siempre antes de calcular una regresión, analizar la existencia de esos posibles valores anómalos, excesivamente alejados del resto de los datos de la nube de puntos?
¿No hay que mirar siempre con mucho detenimiento a la nube de puntos, antes de hacer cualquier otra cosa?
Autora: Mónica Escudero Baylín (monica.escudero@enebro.pntic.mec.es)