CORRELACION

III.    Medida de la correlación. Coeficiente de correlación.

IV.    Distribuciones bidimensionales con frecuencias.

III.    Medida de la correlación. Coeficiente de correlación.

La suma de los productos de las desviaciones de los puntos respecto al centro de gravedad constituye una medida de la correlación correspondiente. Pero es preciso dividirla por el número de puntos para que no dependa de ello. Aún así el coeficiente obtenido no es homogéneo. Para poder comparar la correlación peso-talla en una población de vacas y una población de hormigas podemos dividir el coeficiente por las dos desviaciones típicas correspondientes. de esta forma se obtiene un coeficiente de correlación que varía entre -1 y 1. Esta forma de homogeneizar permite comparar correlaciones de poblaciones diversas.

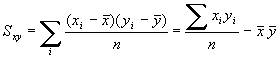
En la siguiente ventana gráfica se muestra la nube de puntos correspondiente a una distribución bidimensional. En el margen inferior puedes modificar las abscisas x de cada punto en el margen izquierdo sus ordenadas y. Puedes aumentar el incremento con el control "inc" de la línea superior. En el gráfico se muestran los valores que intervienen en el cálculo del coeficiente de correlación. A partir de ellos puedes calcular por tu cuenta dicho coeficiente. En la línea superior de la ventana aparece un pulsador "mostrar" si contiene un 1 se mostrará el coeficiente de correlación. Modifica los puntos y observa su efecto en los valores mostrados. Construye "nubes positivas, negativas, amorfas..."

ACTIVIDADES

3     Halla el coeficiente de correlación de las distribuciones a, b, c, d propuestas en la actividad 1. Anota tus resultados en el cuaderno de trabajo. Si aparece un 1 en el control "mostrar" de la parte superior de la ventana se mostrará el valor de la covarianza S_xy y del  coeficiente de correlación r. Pero inicialmente debes fijar su valor en 0 ( para no mostrarlos ) y hallarlo manualmente o con tu calculadora.

4    La siguiente ventana gráfica genera distribuciones aleatorias y muestra los valores necesarios para hallar el coeficiente de correlación correspondiente. Cada vez que pulses el botón inicio o modifiques el número de puntos se generará una nueva distribución. Genera 4 distribuciones aleatorias, anota en el cuaderno de trabajo los valores auxiliares correspondientes y obtén a partir de ellos el coeficiente de correlación. Si aparece un 1 en el control "mostrar" de la parte superior de la ventana se mostrará el valor del coeficiente de correlación. Escribe también en el cuaderno de trabajo el coeficiente de correlación.

IV.    Distribuciones bidimensionales con frecuencia.

Es difícil que en una muestra pequeña de individuos coincidan varios con el mismo peso y talla simultáneamente. En ese caso los puntos de la nube correspondiente aparecerían superpuestos y no se distinguirían. Para el caso de distribuciones bidimensionales con frecuencias suelen utilizarse gráficos tridimensionales o bien aumentar el tamaño de los puntos de la nube de forma proporcional a su frecuencia. El cálculo del coeficiente de correlación puede simplificarse multiplicando los valores pertinentes por las correspondientes frecuencias.

ACTIVIDADES

8    Considera la siguiente distribución bidimensional donde se incluyen en la última fila las frecuencias. Modifica los valores de la última fila de la siguiente ventana gráfica y observa el resultado tanto gráfico como numérico.

Ver  RECTA DE REGRESIÓN