

LA RAZON AUREA
I-¿Qué es la razón áurea?
En un pentágono regular el cociente entre una de sus diagonales (por ejemplo BE) y un lado (por ejemplo CD) es constante. Este cociente o razón se llama la razón áurea. El número que resulta F=1,61803398875.... se llama número áureo o número de oro. (A F también se le representa por la letra griega F)
1-Observa la figura.
En la figura está dibujado un pentágono regular de lado 5 unidades y su circunferencia circunscrita. Una cualquiera de sus diagonales mide 8.0901701, con una precisión de 7 cifras decimales. ¿Cuanto vale el cociente o razón BE/CD? ¿Qué relación tiene con el número F? ¿Explica la diferencia entre los decimales del número F del texto y el resultado F obtenido en la figura?
2.-Al variar el lado obtienes distintos pentágonos regulares? (Utiliza la línea de entrada para introducir distintos valores del radio) Prueba con los siguientes valores del lado
lado = 3 , 3.5 , 1, 2.67
Comprueba que en un pentágono regular el cociente o razón
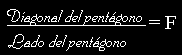
es constante y vale F=1,618034
3-¿Cuanto tiene que valer el lado para que la diagonal valga 1?
Pulsando con el ratón en los vértices del polígono obtienes las coordenadas de los puntos con una precisión de tres decimales.
4-Calcula el lado CD y la diagonal BE con dos decimales. Utiliza para ello la fórmula de la distancia euclídea.
5-Calcula la razón áurea con los datos obtenidos.
6-Compara los resultados con los datos que se te ofrecen en el dibujo.
II-La Divina Proporción
En un pentágono regular si D es la medida de una diagonal y L la medida de un lado se cumple la relación siguiente:
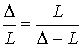
o dicho en palabras: La diagonal (D) es al lado (L) como el lado es a la diferencia entre la diagonal y el lado. (También se dice que el lado es media proporcional entre la diagonal y la diferencia entre la diagonal y el lado)
La formula anterior es una igualdad entre dos razones, es decir es una proporción. El matemático italiano Luca Pacioli entusiasmado por sus propiedades la llamó la proporción divina. Nombre con el cual se conoce aún esta relación.
7.-Comprueba que se cumple la relación para diferentes radios. (Puedes variar el radio en la línea de entrada o bien puedes pulsar el botón izquierdo del ratón en el punto A y arrastrar)
Razonemos por qué es cierta esta relación
8-Observa que BP y PE miden igual que los lados del pentágono. ¿Sabes decir alguna razón?
9-Los triángulos BEC y PED son semejantes (Es decir son iguales en forma pero tiene diferente tamaño). Razónalo.
10-Si los triángulos BEC y PED son semejantes Demuestra la relación
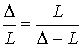
11-Si en la relación anterior, divides el numerador y denominador por L y tienes en cuenta que F= D/L ¿A qué relación llegas?
III-Una relación fundamental
En el apartado anterior has deducido que la razón áurea F cumple la relación
F2 = F+1
o dicho de otra forma F es solución de la ecuación
F2 - F - 1 = 0
A partir de esta relación puedes obtener muchos resultados
12-Calcula el valor exacto de F (indicación: Ten en cuenta que F>1, pues la diagonal es mayor que el lado)
13-Observa que F3 = F2F=(F +1)F= F2 +F =1+F+F.
Es decir F3 = 2F+1
14-Encuentra expresiones para F4 y F5 análogas a las anteriores
15-Halla una expresión para el inverso de F (Indicación: vuelve a la relación fundamental)
16-Calcula exactamente el inverso de F
17-Calcula una aproximación de 7 decimales para el inverso de F
18-Encuentra una expresión para F-2 análoga a la del ejercicio 12
IV División de un segmento en una razón dada
Decimos que el punto P divide al segmento AB en la razón r si el cociente
AP/PB = r
Ejemplos
1) Si r = 1 decimos que P divide al segmento AB por la mitad
2) Si r = F la razón áurea decimos que el segmento AB se ha dividido en extrema y media razón o que hemos realizado la división áurea del segmento AB.
Notas
1- Si hemos realizado la división áurea del segmento AB, decimos que el segmento AP es la sección áurea de AB.
2-El nombre de división en extrema y media razón procede de Euclides.
3-Recuerda que las diagonales de un pentágono regular se cortan según la razón áurea.
19-Divide el segmento AB en las siguientes razones
r: 1.5, 2, 0.1, 0.25
V Construcción de la sección áurea de un segmento
Un problema clásico es construir, con regla y compás, la sección áurea de un segmento dado.
En la escena se pueden observar las sucesivas etapas.
1) Se construye la perpendicular al segmento AB que pasa por B y con el compás hallamos el punto C tal que AB = BC
2) Construimos el punto medio del segmento BC y lo llamamos D
3) Con la regla construimos el segmento AD
4) Con centro en D y radio DB trazamos un arco de circunferencia y calculamos E
5) Con centro en A y radio AE trazamos un arco de circunferencia y calculamos P
El Punto P divide al segmento AB en la razón áurea y el segmento AP es la sección áurea del segmento AB.
20-Siguiendo las instrucciones anteriores, construye en una lámina de papel la sección áurea de un segmento dado.
21-Observa la escena para diferentes longitudes del segmento AB (Puedes cambiarlo en la línea de entrada o arrastrando el punto B)
VI-El símbolo Pitagórico
Si unes los vértices de un pentágono regular de dos en dos trazando las diagonales obtienes la estrella de cinco puntas. Los lados de la estrella son las diagonales del pentágono. Las cuales sabemos que se cortan según la razón áurea.
Los pitagóricos estaban tan orgullosos de las propiedades de la razón áurea que la estrella de cinco puntas era su símbolo.
22-Obtén diferentes tamaños de la estrella de cinco puntas al variar el radio de la circunferencia.
Autor: Julio Castiñeira Merino
| Alumno | |
| © Ministerio de Educación y Ciencia. Año 2001 | |
| Alumno |