MOVIMIENTOS EN EL PLANO

Movimientos     Traslaciones      Giros      Simetrías

Simetría central

En el dibujo, la figura superior (figura 1) se transforma en la figura inferior (figura 2). Se han señalado algunos puntos en la figura superior, figura 1, (A, B, C, D) y los correspondientes en la figura inferior, figura 2, (A', B', C', D'), transformada de la figura 1, mediante una simetría central.

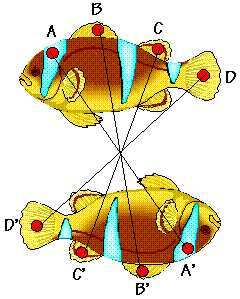
Si te fijas puedes observar que los puntos A', B', C' y D' se obtienen a partir de los A, B, C y D trazando las rectas OA, OB, OC y OD, O es el centro de simetría, y llevando estas distancias, a partir de O, sobre las semirrectas correspondientes. A este movimiento se le llama simetría de centro O.

En la escena siguiente están representados varios puntos y los transformados mediante una simetría central de centro O (0, 0). Comprueba cómo cambian las posiciones de los puntos simétricos al variar el centro de simetría (parámetros Xo e Yo).

1.- ¿Cuál sería el transformado en esta simetría del centro de simetría C (0,0)?. ¿Y la figura transformada de una circunferencia de centro el origen de coordenadas?.

2.- Observa la escena y anota las coordenadas de los puntos simétricos de A (-6, 2), B (-3, -2), C (2, 4), D (4, -3); A', B', C' y D'. ¿Cuáles serían las coordenadas del simétrico del punto P (x, y) ?.

3.- Traslada el centro de simetría al punto (-2, 0). Anota las coordenadas de los simétricos de los puntos A, B, C y D anteriores?. Escribe las coordenadas del simétrico del punto P (x, y).
    Tomando como centro de simetría el punto (0, 1). Calcula las coordenadas de los simétricos de los puntos A, B, C y D anteriores?. Escribe las coordenadas del simétrico del punto P (x, y).

4.- Traslada ahora el centro de simetría al punto (2, -1). Calcula de nuevo las coordenadas de los simétricos de los puntos A, B, C y D anteriores?. Escribe las coordenadas del simétrico del punto P (x, y).
    Si el centro de simetría es el punto C (a, b), ¿cuáles serían las coordenadas del simétrico del punto P (x, y)?

   Simétrico de un segmento

Para obtener el simétrico de un segmento es suficiente calcular los puntos simétricos de los extremos y unirlos. En la escena siguiente se representa el segmento AB y el simétrico A'B' mediante la simetría de centro el origen de coordenadas O (0, 0). Puedes cambiar el centro de simetría (parámetros Xo e Yo) y las coordenadas del extremo B (parámetros Xb e Yb).

5.- Comprueba que las longitudes de un segmento AB y de su simétrico A'B' se mantienen iguales (Utiliza los parámetros Xb e Yb para cambiar el extremo del segmento).
    ¿Qué ocurre con el segmento A'B' cuando el punto B coincide con el centro de simetría? ¿Cuál es, en este caso, el simétrico del punto B?.

6.- Cambia la posición del punto B y anota las coordenadas de los extremos del segmento. Si el punto A (x1, y1) y B (x2, y2), ¿cuáles son las coordenadas de los simétricos A' y B'.

7.- En los enunciados siguientes, elige la respuesta adecuada:
    El transformado de un segmento en una simetría central es otro segmento de: a) la misma longitud, b) mayor longitud que el inicial, c) de longitud menor que el inicial
   (puedes utilizar los parámetros Xb e Yb para construir segmentos horizontales y verticales que te pueden ayudar en la resolución de esta cuestión).
    Un segmento y su simétrico son a) paralelos, b) coincidentes, c) se cortan.

8.- ¿Cuál sería la figura transformada, mediante una simetría de centro O (-5, -2) de una circunferencia de centro el punto O?.

   Simétrica de una recta

Para obtener la recta transformada mediante una simetría de centro O, hay que calcular los simétricos de cada uno de los puntos de la recta r. En la práctica, puesto que una recta queda determinada por dos de sus puntos, es suficiente aplicar la simetría a dos puntos de la recta y unirlos. De esta forma se obtiene la recta simétrica r'.

En la escena siguiente se representan una recta r y su transformada r' mediante una simetría de centro el punto C (2, 1). Puedes cambiar el ángulo de giro (parámetros Xo e Yo), la ordenada del punto B (parámetro Yb) y la inclinación de la recta r (parámetro m).

9.- Comprueba que al desplazar el punto B (utiliza el parámetro Yb), la recta r cambia de posición. Cambia la inclinación de la recta r (parámetro m). Observa los cambios en la recta simétrica.
    Una recta y su simétrica son a) paralelas, b) coincidentes, c) secantes.

10.- ¿Qué ocurre cuando el punto B coincide con el centro de simetría?.

11.- Ajusta la inclinación a 0. ¿Cuál es ahora la recta r? ¿Y la simétrica?.
    Pulsa el botón inicio y calcula las ecuaciones de las rectas r y r' para los valores que se muestran. ¿Qué relación existe entre las pendientes?.

   Simétrico de un ángulo

Para hallar el simétrico de un ángulo hay que calcular el simétrico de cada uno de los dos lados que lo forman. El vértice vendrá determinado por la intersección de los dos lados.

En la escena siguiente se representan un ángulo a y el ángulo transformado a' mediante una simetría de centro el punto C (-3, 0). Puedes cambiar las coordenadas del centro (parámetros Xo e Yo), la posición del punto B (parámetro ordenada) y la amplitud del ángulo a (mediante el parámetro m).

12.- Los lados del ángulo simétrico a', son, con respecto a los lados del ángulo a: a) Paralelos, b) Perpendiculares, c) Coincidentes.
    En consecuencia los ángulos a y a', son: a) iguales, b) a > a', c) a < a'.
   

13.- ¿Qué ocurre si el vértice del ángulo, B, coincide con el centro de giro? ¿Se siguen manteniendo las respuestas dadas en el apartado 12?.

14.- Los elementos que no varían al aplicarles una simetría se denominan invariantes o dobles en la simetría.

En los enunciados siguientes, elige la respuesta adecuada:
    La simétrica de una recta es otra recta: a) paralela, b) coincidente, c) secante.
    Los elementos dobles en una simetría central son: a) las rectas que pasan por el origen, b) Los segmentos paralelos al eje de abscisas, c) el centro de simetría.

15.- Hasta ahora hemos visto que la simetría central conserva las distancias y los ángulos.

En los enunciados siguientes, elige la respuesta adecuada:
    La figura simétrica de un cuadrado es un cuadrado: a) del mismo lado, b) de lado mitad, c) de lado doble.
    La figura simétrica de un rectángulo, es: a) un cuadrado, b) un rombo, c) un rectángulo pero con lados de longitud distinta del original, d) un rectángulo con las mismas medidas de los lados.

16.- Entre los giros de centro el punto C (x, y) existe uno que produce la misma transformación que la simetría de centro C (x, y), investiga cuál debe ser el valor del ángulo de giro para que coincidan las dos transformaciones.

Movimientos     Traslaciones      Giros      Simetrías

Autor: Belarmino Corte Ramos