
TEOREMA DEL SENO
En un triángulo cualquiera se cumple siempre que:
![]()
Tenemos tres igualdades que nos relacionan los seis datos de un triángulo y que nos van a ayudar a resolverlos.
T
Sitúate con el ratón sobre los vértices del triángulo, pínchalos y muévelos. Observa cómo varían los valores de los cocientes dando el mismo resultado. Comprueba en tu cuaderno y con ayuda de la calculadora que esto es cierto para los triángulos que te van apareciendo en la pantalla.
Si quieres ver la demostración del teorema pulsa aquí
Con esto ya estamos en condiciones de empezar a resolver problemas de al menos 2 tipos:
1a. Resolución de un triángulo
del que se conocen dos ángulos y el lado que los une.
Si de un triángulo conocemos A=30º, B=100º y c=5
cm calcular el resto de los elementos. Intenta poner en la escena estos datos, quizá tengas
que cambiar la escala. Observa en la escena los datos que tienes y los que te faltan.
>
Intenta resolverlo en tu cuaderno y comprueba las soluciones pulsando aquí
Modificar en la escena los valores de A, B y c, para ver el planteamiento de los posibles problemas que encontrarás en EJERCICIOS
1b. Resolución de triángulos en los que conocemos dos ángulos y un lado que no sea el que une estos ángulos. En realidad es el mismo caso de antes, pues si conoces dos ángulos conoces el tercero.
Resolver en tu cuaderno, por
ejemplo, el
triángulo A=80º, C=30º y c=8 m. (Puedes ver la solución aquí)
Modificar en la escena los valores de A, B
y c, para ver el planteamiento de los posibles problemas, que encontrarás en EJERCICIOS
2. Resolución de triángulos conocidos dos lados y el ángulo opuesto a uno de ellos. Es el caso que más problemas plantea, pues podemos encontrarnos casos en los que tengamos una solución, dos soluciones o ninguna:
Observa la escena. Puedes mover el lado
b variando el valor de A (parte inferior de la escena). Con esa longitud de b no obtienes
un triángulo, luego el problema no tendría solución, pero si prolongas lo
suficiente la longitud de b, puedes tener una solución o incluso dos
con el
mismo valor de b.
Modifica ahora el ángulo B para que sea
obtuso. En este caso por mucho que modifiques la longitud de b sólo obtienes una
solución.
Ahora intenta demostrar esto en tu
cuaderno utilizando el teorema del seno (recuerda que A+B+C=180º y que el seno nunca
puede ser mayor que 1 o menor que -1).
Resuelve el triángulo del que conocemos
b=7.7 cm., c=8.7 cm. y B=52º. Modifica
la escena hasta que aparezcan esos datos, mueve luego el lado b y apunta en tu
cuaderno lo que observas.(Puedes ver la solución aquí)
Pero aún podemos ir más lejos y
preguntarnos a qué es igual el cociente del teorema de los senos ![]() Pues bien se cumple que:
Pues bien se cumple que:
![]()
donde R es el radio de la circunferencia
circunscrita al triángulo
Mueve el vértice C y
observa cómo son todos los triángulos que se van formando, compara el triángulo ABC con
el ABD. Observa que en este triángulo el ángulo B=90º, es un triángulo rectángulo y
sen90º=1 ¿serías capaz de demostrar la fórmula con estos datos?. Inténtalo y luego
puedes verla aquí. También puedes mover los otros vértices A y B y obtendrás el
triángulo que desees.
Autor: José Ángel López Mateos.
I.E.S.Dámaso Alonso
DEMOSTRACIÓN DEL TEOREMA DEL SENO
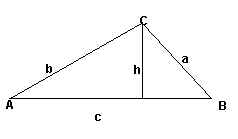
Como ya sabes por la definición de las razones trigonométricas:
h=b·senA, y h=a·senB
luego b·senA=a·senB, de donde se obtiene una de las igualdades del teorema del seno:
![]()
La otra se obtiene igual considerando otra de las alturas del triángulo.
Si el triángulo es obtusángulo se demuestra igual:
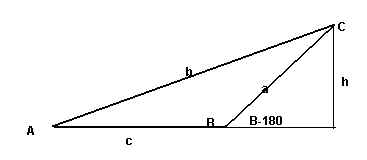
Se demuestra igual pues h=a·sen (B-180º), pero sen (B-180º)=sen B
El teorema del seno se cumple tanto para el triángulo negro ABC, como para el rojo ABD. En este último observa que el lado opuesto a B es el diámetro de la circunferencia, luego 2R, por tanto tenemos:
![]() y como
sen90º=1
y como
sen90º=1 ![]() , por otro lado observa que
D=C, luego sen D=sen C, de donde se obtiene la fórmula:
, por otro lado observa que
D=C, luego sen D=sen C, de donde se obtiene la fórmula:
Soluciones ejercicios:
1.a: Como A+B+C=180º tenemos que C=180-A-B=180-30-100=50º
Para el cálculo de las longitudes de los lados utilizaremos el teorema del seno:
![]() y
despejando
y
despejando ![]() y b se calcula igual
y b se calcula igual
1.b. Como A+B+C=180º tenemos que C=180-A-B=180-80-30=70º
Para el cálculo de las longitudes de los lados utilizaremos el teorema del seno:
![]() y
despejando
y
despejando ![]() y del mismo modo
y del mismo modo ![]()
2.Aplicando el teorema del seno se
obtiene ![]() ,
,
Luego C=62.9º o bien C=117.1º, el problema tiene dos soluciones.
Para C=62.9º A=180-B-C=65.1º y ![]() cm.
cm.
Para C=117.1 se tiene A=10.9º y a=1.8477348 cm.