1.- Practica con cada uno de ellos. Intenta resolver los triángulos siguientes:

A=45º , B=75º , c=5	A=70º ,   b=4'5 , c=5	b=9 , a=7 , A=45º
a=8 , b=4 , A=40º	b=6 , a=4 , A=50º	a=4 , b=5 , c=7

2.- Investiga las condiciones que deben cumplir los datos, en los distintos casos, para que sea posible la existencia del triángulo.

II) Vamos ahora a intentar resolverlos en el cuaderno y con la calculadora. Pero previamente, además de las razones trigonométricas y la relación entre los ángulos de un triángulo, hay que conocer dos importantes teoremas:

TEOREMA DE LOS SENOS.

Observa la figura y arrastra con el ratón los vértices B o C.  Se van obteniendo diversos triángulos ya resueltos.  Comprueba que en todos ellos siempre se cumple la igualdad entre las razones calculadas debajo.:

Este resultado se conoce como TEOREMA DE LOS SENOS :" En todo triángulo, la razón entre el seno de uno de sus ángulos y el lado opuesto es la misma para sus tres ángulos". Es decir en lenguaje simbólico:

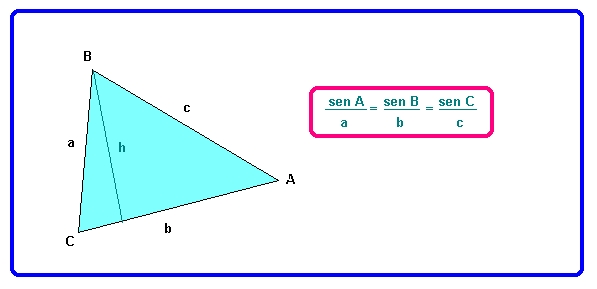
3.- Intenta demostrarlo en el cuaderno. Para ello, con las razones trigonométricas de los ángulos, calcula el valor de la altura h de dos formas distintas e iguala lo obtenido. Repite lo mismo para otras alturas del triángulo.

TEOREMA DEL COSENO.

Observa de nuevo la figura y arrastra con el ratón los vértices B o C.  Se van obteniendo diversos triángulos ya resueltos.  Comprueba que en todos ellos siempre se cumple la relación entre los valores calculados en la parte izquierda del recuadro.

Verifica con la calculadora que se cumple también para los otros lados del triángulo. ¿Qué ocurre si A es un ángulo recto?.

Este nuevo resultado se conoce como TEOREMA DEL COSENO :" En todo triángulo, el cuadrado de un lado es igual a la suma de los cuadrados de los otros dos, menos el doble producto de ambos por el coseno del ángulo comprendido". Es decir en lenguaje simbólico:

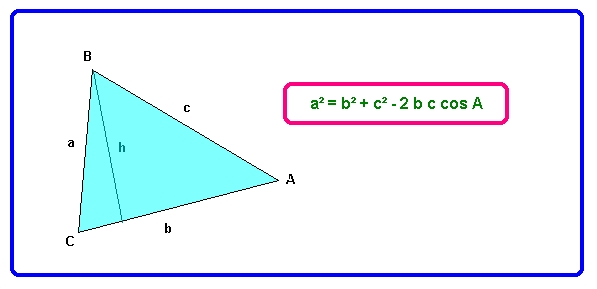
4.- Intenta demostrarlo en el cuaderno. Observa primero que al trazar la altura h se obtienen dos triángulos rectángulos. Ahora, utilizando el teorema de Pitágoras, expresa el valor de a según la altura h y el otro cateto. Luego halla el valor de éste usando los datos del otro triángulo rectángulo, y sustituyendo obtendrás lo buscado.