Introducción a la trigonometría

	Razones trigonométricas
	Geometría

I. Introducción

Consideremos un ángulo determinado y sobre dicho ángulo trazamos rectas paralelas. Los TRIÁNGULOS que se forman son SEMEJANTES pues tienen un ángulo igual y dos lados proporcionales, según Thales, lo que implica que SUS LADOS CORRESPONDIENTES son PROPORCIONALES .

Mueve con el ratón los puntos C y C' y , a continuación, observa qué ocurre con el valor de las distintas proporciones cuando mueves los puntos A y B :

Como has podido comprobar, para un mismo ángulo y un conjunto de segmentos paralelos entre sí, el valor de la proporción entre segmentos se mantiene constante. Para un nuevo conjunto de paralelas, el valor de las seis proporciones no se modifica, aunque se modifiquemos los segmentos AA' y BB'. El valor de las proporciones SOLO DEPENDE DEL ÁNGULO.

II. Definición de las razones trigonométricas

Para unificar criterios, se consideran segmentos perpendiculares a la base de forma que sean triángulos rectángulos. Cada una de estas proporciones recibe un nombre especial, en función de los lados del triángulo que intervienen.

ACTIVIDAD 1. ¿Qué relación existe entre las tres primeras proporciones y las tres últimas?

A todas estas proporciones se las llama RAZONES TRIGONOMÉTRICAS. Las tres primeras proporciones son las principales y las tres siguientes son sus inversas. Reciben los siguientes nombres:

SENO del ángulo a: COSENO del ángulo a: TANGENTE del ángulo a:

COSECANTE del ángulo a: SECANTE del ángulo a: COTANGENTE del ángulo a:

ACTIVIDAD 2. Dibuja en tu cuaderno un triángulo como el de la escena y anota la expresión correspondiente a cada razón trigonométrica

Como: nos centraremos en el estudio del seno, coseno y la tangente.

Además podemos observar que:

III. Definición de las razones trigonométricas en la circunferencia goniométrica

Como hemos visto que la tangente se puede deducir a partir del seno y el coseno, nos centraremos en estas dos razones trigonométricas que, como veremos , tienen similares características.

Ya vimos que el valor de las razones trigonométricas no dependía del tamaño del triángulo, SÓLO DEL ÁNGULO. Si consideramos un triángulo rectángulo en el que la medida de la hipotenusa sea 1 también se mantendrán las proporciones establecidas.

Modifica el valor de la hipotenusa y comprueba como no cambian el seno y el coseno.

ACTIVIDAD 3. Modifica los valores del ángulo y de la hipotenusa y determina qué tipo de valores que toman el seno y el coseno ¿Tienen algo especial? ¿Porqué crees que es así? Anota tus conclusiones en el cuaderno de trabajo

Además, aplicando el teorema de Pitágoras al triángulo tenemos que:

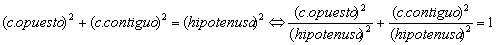
o lo que es lo mismo : que se conoce como FÓRMULA FUNDAMENTAL DE LA TRIGONOMETRÍA

Consideramos una circunferencia centrada en (0,0) y de radio 1 que recibe el nombre de CIRCUNFERENCIA GONIOMÉTRICA . Si tenemos un ángulo y consideramos el punto P en donde corta a la circunferencia, las razones trigonométricas coseno y seno coinciden con la abscisa y ordenada del punto P. En este caso:

Luego en cualquier punto P que se encuentre sobre la circunferencia goniométrica, tenemos que:

senA= ordenada ; cosA= abscisa y por tanto tgA=ordenada/abscisa

Realiza las siguientes actividades con la ayuda de la escena anterior y anota tus conclusiones en el cuaderno de trabajo

ACTIVIDAD 4 Determina los valores del seno y coseno de los ángulos de 90º, 180º, 270º y 360º. Anótalo en tu cuaderno

ACTIVIDAD5. Identifica en qué cuadrantes toma valor positivo el seno del ángulo y en cuáles es negativo

ACTIVIDAD 6. Identifica en qué cuadrantes será positivo el coseno del ángulo y en cuáles será negativo

ACTIVIDAD 7. ¿Cuál será el signo de la tangente en cada cuadrante?

ACTIVIDAD 8. Calcula la tangente de los ángulos de 90º, 180º, 270º y 360º. ¿qué ocurre? ¿por qué?

ACTIVIDAD 9. ¿Cuántos ángulos hay en la circunferencia tales que seno A= 0'5? ¿Y cos A= 0'342? y ¿y senA =-0'875?

	Mª Dolores Marí Puget

	© Ministerio de Educación y Ciencia. Año 2004