|
CONTENIDOS: Dibujo
|
||||||||||||||
|
||||||||||||||
|
2.-
Instrumentos de dibujo o trazado. |
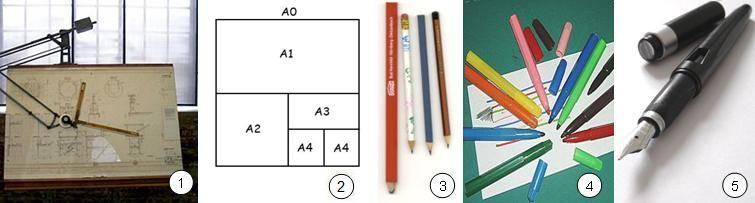 Para poder dibujar necesitamos una serie de instrumentos que nos permitan plasmar nuestras ideas sobre un determinado soporte. Los más importantes son la zona de trabajo (1), soporte papel (2) o soporte electrónico (programas informáticos de dibujo), lápiz (3), portaminas, goma, rotuladores (4) y estilógrafos (5) entre otros. En España utilizamos la serie A para los formatos de papel. En función de las dimensiones y la finalidad de nuestro dibujo, utilizaremos un formato de papel más grande o más pequeño. El formato de referencia es el A0, de dimensiones 1189 x 841 mm, a partir del cuál se obtienen el resto de formatos de papel doblando por la mitad (siempre por el lado más largo). Observando la imagen (2) podemos comprobar fácilmente que A0 = 2 A1 = 4 A2 = 8 A3 = 16 A4. El formato habitual tipo folio más utilizado es el A4. |
|
3.- Instrumentos
auxiliares. |
|||
|
|
4.- Representación
ortogonal: sistema diédrico. |
||||
|
Vamos a suponer el espacio tridimensional dividido por dos planos de proyección, el plano vertical (PV) y el plano horizontal (PH). Estos planos se cortan en la línea de tierra (L.T.) y dividen el espacio en 4 cuadrantes o diedros (primer, segundo, tercer y cuarto cuadrante). Trabajaremos siempre en el primer cuadrante. En diédrico tenemos que proyectar perpendicularmente cada punto P sobre el PV (P1) y el PH (P2). La distancia entre P1 y L.T. es la cota o altura del punto P, mientras que la distancia entre P2 y L.T. se denomina alejamiento.
Para pasar del espacio al papel abatimos el PH. sobre el PV, obteniendo el siguiente resultado:
Para representar una recta en sistema diédrico basta con proyectar dos puntos cualesquiera de la misma. Obtendremos dos proyecciones verticales y dos proyecciones horizontales y, uniendo las proyecciones del mismo nombre, conseguiremos la proyección vertical y horizontal de la recta. Proyectaremos perpendicularmente el punto P sobre el PV (P1) y el PH (P2). De igual forma proyectaremos el punto T para obtener T1 y T2. Uniendo las proyecciones del mismo nombre, es decir, P1 con T1 y P2 con T2, obtendremos las proyecciones r1 y r2 de la recta:
Para pasar del espacio al papel abatimos el PH sobre el PV, obteniendo el siguiente resultado:
En determinadas ocasiones, puede ser necesario realizar una tercera proyección sobre un plano lateral o de perfil (proyección lateral o de perfil), sobre todo para aquellas figuras más complicadas que requieran tres vistas en lugar de dos para quedar perfectamente definidas. Cuando tenemos tres planos perpendiculares entre sí (PV, PH y PP) que se cortan dos a dos, se forma un triedro. Cada punto del espacio es ahora proyectado sobre tres planos, el PV (obtenemos P1) el PH (obtenemos P2) y el PP (obtenemos P3):
Para pasar del triedro espacial al plano papel abatimos el PH y el PP de manera que coincidan con el PV:
Cuando colocamos un objeto tridimensional en el triedro y proyectamos sus caras sobre los tres planos de proyección, PV, PH y PP, obtenemos el alzado, planta y perfil de la figura. El alzado es la proyección sobre el PV, la planta es la proyección sobre el PH y el perfil es la proyección sobre el PP.
Nuevamente, desabatiendo los planos obtendremos las proyecciones sobre el plano papel:
|
|
5.- Perspectiva caballera. |
|||
Cuando ya tenemos colocados los ejes del sistema de coordenadas, proyectaremos sobre los planos de forma perpendicular para obtener las proyecciones de cada una de las caras de la figura:
Abatiendo los planos obtendremos las 3 proyecciones principales de la figura (alzado, planta y perfil) en el plano papel:
|
|
6.-
Normalización y metrología. |
|||||
|
El calibre o pie de rey se compone de
una regla fija graduada en milímetros y otra regla deslizante llamada nonio,
nonius o vernier. Los nonius pueden ser de diferentes precisiones, pero en 1º de
ESO emplearemos el más común, el NONIUS DECIMAL, capaz de medir hasta décimas de
milímetro.
|
|
Para que un objeto, figura, etc, quede perfectamente representado, debemos dibujar las 3 vistas del mismo (podrían ser necesarias hasta 6 vistas) o su perspectiva en 3 dimensiones. Incluso a veces, debido a la complejidad de la figura, es recomendable dibujar tanto las vistas como la perspectiva en 3 dimensiones. En cualquier caso, es imprescindible para la fase de construcción o fabricación, disponer los planos con las correspondientes medidas y dimensiones. Acotar consiste en implementar en los planos de nuestra figura las medidas de cada una de sus partes y componentes.
|
|
|
|
|
11.- Recursos
utilizados. |
|