
 |
Ángulos de un polígono |
| Geometría | |
| 1. ángulos interiores Y EXTERIORES | |
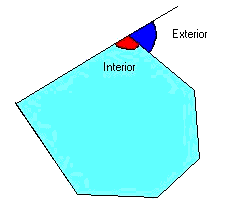
| En un polígono se
contemplan dos tipos de ángulos: los interiores y los exteriores. Los interiores son los formados por cada dos lados contiguos y los exteriores son sus suplementarios. Conocemos la suma de los ángulos interiores de cualquier triángulo, que es 180º. Como cualquier polígono se puede dividir en triángulos se podrá calcular cuál es la suma total en cada caso. Un cuadrilátero se
puede dividir en 2 triángulos, un pentágono en 3, un hexágono en 4, etc.; siempre dos menos que el número de lados. En
definitiva, un polígono de n lados se puede descomponer en n-2 triángulos y, por tanto, la
suma de los ángulos interiores será: 180º·(n-2). Si el polígono es regular el valor de uno de los ángulos
interiores es:
La suma de los ángulos exteriores de cualquier polígono es 360º. Teniendo en cuenta que el ángulo interior y el exterior suman 180º, en un polígono de n lados los interiores y los exteriores sumaran, en total, n·180º, como los interiores suman 180º·(n-2) los exteriores suman 360º |
 |
| 1.- Observa que cada ángulo exterior de un triángulo coincide con el siguiente y cómo los tres dan una vuelta completa, igual pasa con los cuatro del
cuadrado y los cinco del pentágono, etc.
2.- Aumenta el número de lados del polígono y mira la disminución que sufren los ángulos exteriores así como el aumento de los interiores. 3.- Calcula el valor de los ángulos interiores y exteriores de polígonos regulares de 20 y 40 lados. Compruébalo en la escena Descartes. 4.- Dibuja en tu cuaderno polígonos no regulares, señala los ángulos exteriores y observa cómo se cumple la misma propiedad.
|
|
| 2. Ángulo central en un polígono regular | |||
| Si pensamos en el polígono inscrito en una circunferencia el ángulo central se corresponde al que forman dos radios consecutivos del polígono. La medida de todos los ángulos centrales es de 360º, la misma que la de los ángulos exteriores. | |||
5.- Calcula en tu cuaderno
la medida del ángulo central de polígonos de 6, 12, 20 y 36 lados. Comprueba en la escena el valor de
dichos ángulos.
|
|||
| Miguel García Reyes | ||
 |
||
| © Ministerio de Educación y Ciencia. Año 2001 | ||