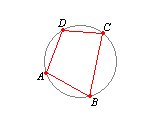
DEFINICIÓN: Un cuadrilátero cuyos vértices son puntos de una circunferencia se dice que está inscrito en ella. Un cuadrilátero es inscriptible si existe una circunferencia que contenga sus cuatro vértice.
REFLEXIONA: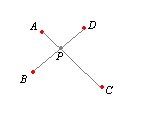
Si un cuadrilátero es inscriptible sus vértices
cumplirán la propiedad de los cuatro puntos concíclicos
entonces trazando las diagonales AC y
BD estás se cortarán en un
punto P interior. Las diagonales representan dos rectas secantes que
pasan por P y la potencia de
P respecto de la circunferencia es
PA
x PC = PB x PD
1º ¿ Cómo averiguar
si un cuadrilátero es inscriptible ?
2º ¿Si es
inscriptible, como determinar la circunferencia ?
DESCUBRIENDO OTRA PROPIEDAD DEL CUADRILÁTERO INSCRIPTIBLE...
Esta propiedad tiene que ver con la relación
existente entre un ángulo inscrito en una circunferencia y el central
correspondiente.
...EXPERIMENTA CON EL NIPPE DESCARTES...
Podrás experimentar que cuando un cuadrilátero es inscriptible los ángulos opuestos son suplementarios.
Los ángulos A y C son opuestos y su suma A + C = 180º. Posiciona los puntos donde quiera que sea, son controles que podrás pinchar y arrastrar con el ratón sobre la circunferencia y comprueba que la relación entre ángulos apuestos es la dicha antes.
¿ Tiene esto que ver con el hecho de que el central correspondiente a un ángulo inscrito mide el doble que éste?
Observa el NIPPE DESCARTES en las condiciones iniciales. ¿Cuánto mide el central correspondiente a A? ¿Cuánto medirá el central correspondiente a C?
¿Cuánto suman los centrales correspondientes a A y a C?
Cambia la posición de los puntos y responde a las preguntas anteriores.
¿Explica esto la propiedad anunciada?
3º Coge
tu cuaderno y
trata de demostrar esta propiedad.
REFLEXIONA...
La suma de los ángulos interiores de un cuadrilátero cualquiera, inscriptible o no, suman 360º
Pero por el hecho de ser inscriptible la suma de ángulos opuestos no puede ser cualquier otra que 180º
La propiedad de ser inscriptible añadida al cuadrilátero ha introducido una limitación al valor de los ángulos.
... SIGUE EXPERIMENTANDO CON EL SIGUIENTE NIPPE...
Inicialmente el cuadrilátero no es inscriptible. Observa que la suma de los ángulos B+D no es 180º.
Se han trazado las mediatrices a los lados AB y BC. Y el corte O de ambas tendrá que ser el centro de la circunferencia. Se cumple que OA = OB = OC = r pero OD no mide los mismo por tanto los cuadro vértices no son concíclicos y el cuadrilátero no queda inscrito.
Si quieres ver la circunferencia donde deben estar situados los cuatro vértices escribe en la ventana de parámetros el valor que debe tener el radio (r = 4.69) y pulsa el botón "limpiar".
Si desplazas el punto D hasta colocarlo en la circunferencia entonces B + D = 180º.
Puedes para ello desplazarlo con el ratón o modificar las coordenadas del punto (D.x,D.y) desde la ventana de parámetros.
Es evidente que la posición del vértice D puede ser cualquiera del arco AC.
Prueba a colocar el vértice en otras posiciones, manteniendo las de inicio de A, B y C, hasta hacer el cuadrilátero inscriptible.
Cambia el radio a valor 0 y pulsa el botón "limpiar".
Cambia la posición de A, B y C y haz inscriptible el cuadrilátero. Recuerda que para conseguirlo tienes que ir mirando la suma B+D. También te servirá dibujar la circunferencia escribiendo el nuevo valor del radio y pulsando el botón "limpiar"
Dibuja un cuadrilátero inscriptible tal que AB=4, BC=5. ¿Cuánto vale el ángulo en B y en C? ¿Cuánto miden los otros dos lados? ¿Hay más soluciones? Obtén al menos una más.
Al final borra la circunferencia y pulsa el botón inicio.
REFLEXIONA...
Un cuadrilátero rectángulo ¿es siempre inscriptible?
Prueba a formar un rectángulo (cuatro lados paralelos dos a dos), por ejemplo haciendo AB=CD=6 y horizontales y AD=BC=4 verticales, para facilitar la construcción. ¿Qué pasa con la suma B+D? Dibuja otro rectángulo y hazte la misma pregunta.
5.-
Coge tu cuaderno, dibuja un rectángulo y trata de demostrar que es inscriptible
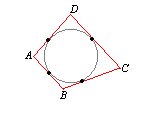
DEFINICIÓN: Un cuadrilátero está cinscunscrito a una circunferencia cuando sus lados son tangentes a ella.
Desde otro punto de vista la circunferencia quedará inscrita en el cuadrilátero pues en cada lado existe un punto y solo uno que pertenece a la circunferencia.
Vamos a descubrir la propiedad que caracteriza a un cuadrilátero circunscribible, pues no todo cuadrilátero lo es.
OBSERVA LA FIGURA ANTERIOR...
Ahora hay que fijarse en que los lados
AD y
AB son tangentes trazadas desde el punto A a la
circunferencia y los lados
CB y
CD son tangentes trazadas desde
C. ¿Recuerdas que decíamos de las rectas
tangentes a una circunferencia trazadas desde un punto exterior ella?
¿Cómo son las longitudes de los segmentos limitados entre
A y los puntos de
tangencia? ¿Y las longitudes de los segmentos limitados entre
C y los puntos de
tangencia?
EXPERIMENTEMOS CON EL SIGUIENTE NIPPE DESCARTES...
OBSERVAR:
En la figura inicial del Nippe se ha dibujado un cuadrilátero que no es circunscribible.
Se ha dibujado las bisectrices de los ángulos A y B. Su punto de corte deberá ser el centro de la circunferencia sobre la que debiera estar circunscrito el cuadrilátero.
El valor del radio de esta circunferencia es, para este caso, 3. Y si quieres verla basta que introduzcas este valor en la ventana de parámetros y después pulsar el botón de Limpiar.
Se comprueba que el cuadrilátero no queda circunscrito a la circunferencia.
Comprueba además que la suma de los lados opuestos no es la misma, es decir AB + CD no es igual a BC + DA.
Ahora vas a cambiar las longitudes de los lados hasta conseguir que la suma AB + CD sea igual a BC + DA. Para ello desplaza los controles colocados en los vértices hasta que los consigas. En ese momento observa el valor que tiene el radio y dibuja la circunferencia, como lo hiciste antes: introduce el valor del radio en la ventana de parámetros y pulsa limpiar.
Comprobarás que el cuadrilátero ha quedado circunscrito a la circunferencia es decir has obtenido un cuadrilátero circunscribible.
Repite el ejercicio, variando las longitudes de los lados AB, BC, CD y DA y asegúrate que cuando el cuadrilátero es circunscribible, se cumple AB + CD = BC + DA.
La condición necesaria y suficiente para que un cuadrilátero sea circunscribible es que la suma de los lados opuestos valga lo mismo.
REFLEXIONA:
Has comprobado que cuando la suma de los lados opuestos vale lo mismo el cuadrilátero se puede circunscribir en una circunferencia.
Cumplida la propiedad, el centro de la circunferencia es la intersección de las bisectrices de los ángulos interiores del cuadrilátero.
6.-
Ahora supón que un cuadrilátero está circunscrito a una circunferencia y
trata de demostrar que la suma de los lados opuestos vale lo mismo.
SOLUCIONES:
1º Se trazan las diagonales y se obtiene el punto de corte P. Se calculan los productos PA x PC y PB x PD. Si estos productos son iguales, el cuadrilátero es inscriptible.
2º Se trazan las mediatrices de dos lados, p.e. AB y BC. El corte equidista de A, B y C y es el radio de la circunferencia buscada. El punto D también estará en la circunferencia, pues el cuadrilátero es inscriptible.
3º La recta BD divide al plano en dos semiplanos. Los dos arcos de circunferencia BD sobre distinto semiplano completan la circunferencia es decir suman 360º. Los vértices A y D están en distinto semiplano respecto de la recta BD. Así el ángulo inscrito A medirá la mitad del arco BD del semiplano opuesto (medida del central correspondiente) y lo mismo podemos decir del ángulo inscrito C. Por tanto la suma de los ángulos A+C es la mitad de 360º.
4º Cualquier cuadrilátero se puede dividir en dos triángulos, trazando una diagonal. Como cada triángulo suma 180º el cuadrilátero suma 360º.
5.- Dibuja las diagonales AC y BD, estas son iguales y se cortan en el punto medio. Por tanto este punto equidista de los vértices y será el centro de la circunferencia buscada.
AB + CD = (m + n) + (p + q) = m + n + p + q ; BC + DA = (n + q) + (p + m) = m + n + p + q
Consecuentemente: AB + CD = BC + DA
Autor: Ángel Cabezudo Bueno
 |
||
| © Ministerio de Educación y Ciencia. Año 2000 | ||
