|
Cuadro
Resumen
Todas
las funciones polinómicas de grado menor que 4 son simétricas
|
Simetría
de las funciones polinómicas |
|
Significado
Gráfico |
Significado
Algebraico |
Significado
Polinómico |
|
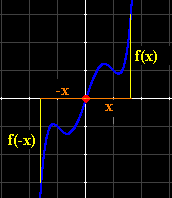
Simetría
respecto de (0,0) |
|
|
Función
impar
|
Función
impar
|
Los
coeficientes de
grado
par de
f(x) son nulos
|
|
|
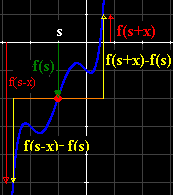
Simetría
respecto de (s,f(s)): punto de la gráfica en que x=s |
|
|
|
Sea
f(x)=axn+bxn-1+...
Si
g es la traslación de f por el vector
(-s,-f(s)),
g(x)=f(x+s)-f(s) es función
impar
|
Los
coeficientes de x de grado par>0 en
f(x+s)
son
nulos, en particular, el coeficiente
de grado
n-1es
nulo, nas+b=0, s=-b/na |
|
g(x-s)=f(x)-f(s)
y g no tiene coeficientes de grado
par,
así, al desarrollar f(x) en potencias de (x-s),
|
Los
coeficientes de (x-s) de grado par>0
de este desarrollo son
nulos |
|
|
|
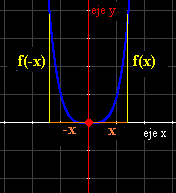
Simetría
respecto del eje-y: x=0 |
|
|
Función
par
|
Función
par
|
Los
coeficientes de
grado impar de
f(x) son nulos
|
|
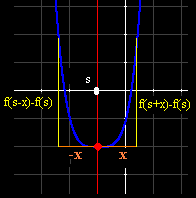
| Simetría
respecto del eje x=s |
 |
|
Sea
f(x)=axn+bxn-1+...
Si
g es la traslación de f por el vector
(-s,-f(s)),
g(x)=f(x+s)-f(s) es función par
|
Los
coeficientes de x de grado impar en
f(x+s)
son
nulos, en particular, el coeficiente
de grado
n-1es
nulo, nas+b=0, s=-b/na |
|
g(x-s)=f(x)-f(s)
y g no tiene coeficientes de grado
impar,
así, al desarrollar f(x) en
potencias de (x-s),
|
Los
coeficientes de (x-s) de grado impar
de este desarrollo son
nulos |
|
|
|
|
Si f(x)=axn + bxn-1 + ... es
simétrica, lo será respecto del punto de su gráfica (si
n impar)
o del eje vertical
(si n par) en que x=-b/na
|
|
|


