
Programación lineal
Aun cuando la programación lineal surgió especialmente para dar respuesta a cuestiones de carácter logístico y militar, es en la industria y en la economía donde posteriormente ha encontrado sus aplicaciones más interesantes.
En los problemas prácticos con los que nos encontramos en el mundo actual intervienen multitud de factores (materia prima, mano de obra, transporte, recursos disponibles, niveles económicos, tiempo, etc.) sujetos a múltiples restricciones, con los que se desea obtener unos beneficios máximos o unos costes mínimos. La parte de la matemática con la que se resuelven este tipo de problemas se llama programación lineal.
Un problema de programación lineal para dos variables consiste en:
optimizar (maximizar o minimizar) una función lineal de la forma:
![]()
que llamamos función objetivo
sujeta a una serie de restricciones, dadas mediante inecuaciones lineales:
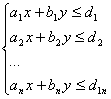
Cada desigualdad lineal anterior determina un semiplano. El conjunto de los puntos que cumplen todas las desigualdades determinan un recinto, acotado o no, que llamamos región factible. Se llama solución óptima a una solución factible que optimice la función objetivo.
El teorema fundamental de la programación lineal dice que la solución óptima se encuentra siempre sobre la frontera de la región factible
Autor: Juan E. Cereijo Viña
| © Ministerio de Educación y Ciencia. Año 2001 | ||