Progresiones geométricas. Teoría.
	3º de E.S.O.

 

Término general. an = a1.rn-1 Demostración.                   Según lo anterior, el término general de la progresión 2, 4, 8, 16,.. será    an = 2·2n-1 Y operando obtenemos:                         an = 2n

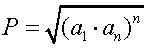
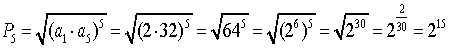
Producto de los n primeros términos. Llamamos P al producto de los n primeros términos de una progresión geométrica con razón positiva (r>0). Demostración.                    Ejemplo. El producto de los 5 primeros términos de la progresión geométrica 2, 4, 8, 16, 32,.... es (Puedes comprobarlo usando la escena que hay en la página de Progresiones geométricas)

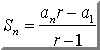
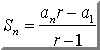
Suma de los términos de una progresión geométrica. Llamamos  Sn   a la suma de los n primeros términos de una progresión geométrica. Demostración.                   Ejemplo. Vamos a calcular la suma de los 10 primeros términos de la progresión aritmética 2, 4, 8, ... 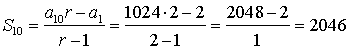Aplicando la fórmula:              Como:     a1 =  2 r = 2 a10 = a1·rn-1 = 2·210-1 = 2·29 = 210 = 1024  (Puedes comprobarlo usando la escena que hay en la página de Progresiones geométricas) Entonces, sustituyendo y operando en la fórmula de la suma:   (Puedes comprobarlo usando la escena que hay en la página de Progresiones geométricas)

Término General. Sean a1, a2, a3, ..... términos de una progresión geométrica de razón r. Por lo tanto, a2 = a1· r = a1· r1 a3 = a2·r = a1·r·r = a1· r2 a4 = a3·r = a1·r2·r = a1· r3  ........................ an = a1· rn-1

Suma de términos. Llamamos Sn a la suma de los n primeros términos de una progresión geométrica. Sn = a1 + a2 + a3 +....... + an-1 + an Multiplicamos por r los dos miembros de la igualdad: Sn·r = a1·r +  a2·r + a3·r +......+ an-1·r + an·r = a2 + a3 + a4 +......+ an + an·r Restamos las dos expresiones siguientes miembro a miembro (observa que los términos que tienen el mismo color, al restar van a desaparecer): Sn·r = a2 + a3 + a4 +......+ an + an·r Sn = a1 + a2 + a3 +....... + an-1 + an ----------------------------------------------- Sn·r - Sr = an·r - a1 Sacando factor común en el primer miembro a Sn: Sn(r - 1) =  an·r - a1 Y, despejando:

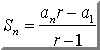
Producto de términos. Utilizaremos la siguiente propiedad de las progresiones geométricas:" El producto de dos términos equidistantes de los extremos es igual al producto de estos" Según lo anterior,  a1·an=a2·an-1=a3·an-2 = ....... Comprueba esta propiedad con la escena que hay debajo.

Con los controles Razón y a1 elige los valores que quieras para formar la progresión. Fija el primer término del producto con el control del mismo nombre. Fija el último término del producto con el control del mismo nombre (Observa que el producto de ambos términos se realiza automáticamente). Avanza un término con el control Primer término y retrocede uno con el control Último término. (Observa que el producto de ambos términos sigue siendo el mismo) Puedes repetir el paso 3. las veces que quieras y comprobarás que el producto no varía. Puedes hacer una nueva elección de términos con los controles correspondientes y repetir el proceso, pulsando previamente Inicio. Puedes cambiar de progresión y comprobar que la propiedad se sigue cumpliendo.

Llamamos  P al producto de los n primeros términos. Es decir, P = a1·a2·a3.......an-1·an y también          P = an·an-1·an-2.......a2·a1 Multiplicando miembro a miembro las dos expresiones, obtenemos: P2=(a1·an)·(a2·an-1)·(a3·an-2).....(an-1·a2)·(an·a1) Aplicando la propiedad vista con anterioridad, todos los paréntesis serán iguales a (a1·an). Por lo tanto, P2 = (a1·an)·(a1·an)·(a1·an)....(a1·an)·(a1·an) = (a1·an)n  y despejando,

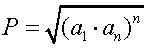
Mª Loreto Ayuso de la Calle   © Ministerio de Educación y Ciencia. Año 2003