NÚMEROS COMPLEJOS
FORMA POLAR
3. Módulo de un número complejo
El módulo de un número complejo es la
distancia que hay desde el origen de coordenadas hasta su afijo. Se representa
por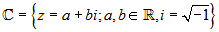 
.
El módulo de un número complejo se calcula aplicando el teorema de Pitágoras.
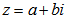
Argumento de un número complejo
El argumento de un número complejo es el ángulo que forma el semieje positivo de abcisas , con la semirrecta que une el origen de coordenadas con su afijo.
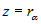
El argumento principal de un número complejo está comprendido entre 0º y 360º.
Forma polar de un número complejo
La forma polar de un número complejo z, es aquella en que se
da el módulo r y el argumento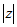 
. Se representa
por .
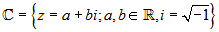Para pasar un número complejo
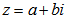a forma polar
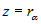es suficiente con hallar el módulo
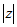y el argumento
.
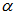3.- Mover el punto P el en plano y comprobar, en puntos sencillos, el valor del módulo y el argumento.
4. Paso de forma binómica a forma polar
Para pasar un número complejo
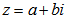a forma polar
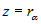es suficiente con hallar el módulo
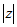y el argumento
.
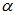Paso de forma polar a forma binómica
Para pasar un número complejo
en forma polar
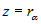a forma binómica es suficiente con
hallar la parte real como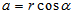 
y la parte
maginaria como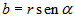 
.
4.-
Mover el punto y hallar la parte real e imaginaria de
, 
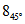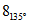y
.
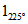La forma trigonométrica de un número
La forma trigonométrica es una variante de la forma polar, también utiliza el módulo y el argumento. Es muy útil para pasar de la forma polar a la forma binómica:
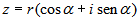
Dado un número complejo en forma polar,
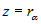, para pasarlo a forma binómica,
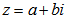, hay que hallar las componentes
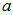y 
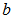. Se
utiliza la definición de seno y coseno.
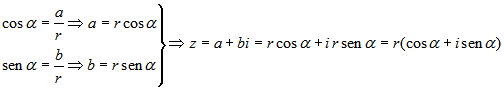
Ir a la tercera parte del tema
| |||||||||||||||
