
Como puedes observar, nuestra definición de tangente no resulta válida pues hay casos que no incluye. En el ejercicio hemos visto una tangente que tiene dos puntos comunes con la curva.
En la siguiente escena se representa una rosa de tres pétalos.
5.- Da a m los siguientes valores: 1.74, -1.74 y 0. Las tres rectas así obtenidas ¿son tangentes o secantes?
En la siguiente escena puedes ver la función seno.
6.- Dale al parámetro c el valor 1
¿Cuántos puntos de tangencia tienen recta y función? Ayúdate disminuyendo la escala
Pero hay más todavía. Vamos a considerar una curva abierta. Observa la siguiente escena
Las dos rectas tienen un punto común con la curva, pero mientras la azul se aparta totalmente de nuestro concepto de tangente, la verde coincide con él.
Como conclusión podríamos decir que la definición aceptada por válida en el aludido concurso es errónea.
Pero entonces ¿qué es una tangente a una curva?
Una forma de llegar a expresar de manera formal el concepto de tangente es la de considerar la tangente como límite de las secantes a la curva que pasan por P (x0,y0).
7.- Disminuyendo el valor de la abscisa desplaza el punto P(x1,y1)) sobre la curva hasta que coincida con P(x0,y0) "y0=f(x0) e y0=f(x0)". En ese momento, la secante y la tangente coinciden. En la parte superior izquierda del applet puedes ver la pendiente de las sucesivas secantes que en el límite es la pendiente de la tangente.
DEFINICIÓN DE TANGENTE A UNA CURVA
La tangente a una curva y = f(x) en el punto P0=(x0, y0) tiene por ecuación
y - y0 = m(x-x0) donde
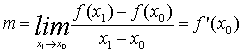
luego la derivada de f en x0 es precisamente la pendiente de la tangente a la curva de ecuación y = f(x) en el punto (x0, f(x0)).
Autor: José Ramón Escudero García
| Asturias | ||
| © Ministerio de Educación y Ciencia. Año 2001 | ||
| Castilla y León |