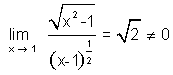2. INFINITÉSIMOS EQUIVALENTES

Análisis.

Bachillerato de la modalidad de Ciencias de la Naturaleza y de la Salud o Tecnológico

2.1  ORDEN DE UN INFINITÉSIMO

Hasta ahora hemos utilizado el concepto de orden de un infinitésimo únicamente para comparar infinitésimos entre sí, pero podemos precisarlo más hasta llegar a su cuantificación, es decir, hasta llegar a medir el infinitésimo. Para ello, como para cualquier medida, necesitamos definir una unidad de medida, un infinitésimo al que adjudicaremos el orden 1 y que nos servirá de referencia para medir los demás:

Se asigna el orden 1 a un infinitésimo α, llamado infinitésimo principal:

el infinitésimo y = x-a  cuando x → a (en particular el y = x si x → 0),

y el infinitésimo y = 1/x cuando x → ∞

Se da entonces la siguiente definición:

Se dice que un infinitésimo f es de orden n si y sólo si   , donde p es un número finito distinto de cero

 

 

Así por ejemplo, las funciones potenciales  y = xn y las funciones y = x1/n son infinitésimos de orden n y 1/n, respectivamente, cuando x → 0.

  

 

Comprueba:

En la escena de la derecha, utiliza el control del grado n de la función y = xn para ver las sucesivas gráficas que se van obteniendo y la diferente rapidez de convergencia a cero.

Utiliza la de más abajo para lo que se ve a continuación.

 
Por su parte, cuando x → 1,   es un

infinitésimo de orden ½, ya que se tiene , lo mismo que

 

 

2.2  INFINITÉSIMOS EQUIVALENTES

Diremos que dos infinitésimos f y g son equivalentes cuando

 
Es decir, que las dos funciones f(x) y g(x) tienden hacia a a la misma velocidad, por lo que en las proximidades de a los valores de f(x) y los de g(x) son casi iguales.

Esto nos permitirá, según veremos en un próximo teorema, sustituir una función por otra en determinadas circunstancias, simplificando con ello de manera muy importante el cálculo de algunos límites.
 

 

Tarea 2:

Aquí tienes unos cuantos infinitésimos. Utiliza los resultados que hemos ido obteniendo en las tareas anteriores y la escena de la derecha, para estudiarlos y hacer parejas de infinitésimos equivalentes cuando x → a.

y = x,   y = sen x,    y = tg x,     y = ln x, y = 2.ln x,     y = 1 - cos x,      y = x2/2, y = ln (1+x), y = x-1

(Debes escribir en la escena las ecuaciones de las funciones que quieras ver, hasta dos cada vez, una tras otra y seguido en cada caso de la tecla "enter" y del botón "inicio".

Además ten en cuenta que aquí, sen es sin, tg es tan, ln es log y que x2 es x^2).

Una vez hecho eso, debes demostrar que efectivamente las conclusiones a las que has llegado son correctas, aplicando la definición anterior y los procedimientos habituales del cálculo de límites.

 

Y para terminar con este breve repaso de los infinitésimos, un teorema que será necesario aplicar más tarde y que es una herramienta muy útil en el cálculo de límites:

Teorema.- Si en la expresión de una función se sustituye un factor o un divisor infinitésimo f por otro equivalente g, el límite de la función no varía.
 

  Cándido Teresa Heredia
 
© Ministerio de Educación y Ciencia. Año 2004