Asíntotas verticales

	ASÍNTOTAS
	Análisis

1. RAMAS INFINITAS Y ASÍNTOTAS

Las ramas infinitas de una función se dan cuando la x, o la y=f(x), o ambas tienden a infinito.

Cuando la curva se acerca a una recta cuando x o y tienden a infinito, dicha recta se llama ASÍNTOTA de la gráfica, cuando no se acerca a ninguna recta se llama RAMA PARABÓLICA.

	ASÍNTOTA VERTICAL
	ASÍNTOTA HORIZONTAL

Volver al índice

1.1.- Asíntotas verticales

En esta escena está representada la función

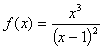y su asíntota vertical x=a.

También está representada otra recta vertical x=k.

Le puedes dar al parámetro k el valor adecuado para que la recta x=k coincida con la asíntota vertical de la curva, x=a. O bien puedes introducir directamente el valor de k en la ecuación x=k y pulsar ENTER. De esta forma se superpondrá la recta verde sobre la azul, que es la asíntota correcta.

1.- ¿Cuál es el límite de la función cuando xa? Para averiguarlo puedes ayudarte de la escena moviendo el punto P, cambiando su abcisa P.x

¿Cuánto vale la y del punto P si x=a?

Con este ejemplo habrás observado que la asíntota vertical tiene de ecuación x=1

Justamente el valor de x que hace cero el denominador.

Por tanto para averiguar las asíntotas verticales de una función, basta igualar a cero el denominador. Las soluciones de la ecuación resultante serán asíntotas verticales, si no se anula también el numerador.

EJERCICIO 1

Averigua las ecuaciones de las asíntotas verticales de las siguientes funciones, ayudándote de la escena adjunta.

a)
b)
c)

¿Cuál es el límite de cada una de estas funciones cuando xa por la izquierda y por la derecha?

De nuevo te puedes ayudar de la escena dando a la abcisa de P, P.x valores cada vez más próximos a a, por la izquierda o por la derecha.

	Ángela Núñez Castaín

	© Ministerio de Educación y Ciencia. Año 2001