
 |
TASA DE VARIACIÓN INSTANTÁNEA |
| Análisis | |
| 1. EVOLUCIÓN DE LA VELOCIDAD MEDIA | ||
|
Cuando circulamos en un coche podemos mirar en cualquier momento la velocidad que marca el velocímetro y decimos " en este momento voy a 120 km/h". Esa velocidad representa intuitivamente la velocidad instantánea . Si queremos definirla a partir de la relación espacio recorrido y tiempo empleado en recorrerlo tenemos un problema porque ese tiempo sería cero y el espacio también. Sin embargo podemos recurrir a la idea de límite y considerar las velocidades con que hemos recorrido trayectos cada vez más pequeños. Parece razonable que, si esos trayectos se van acortando hasta el cero, las velocidades medias se irán aproximando a la velocidad con que circulo en un instante determinado.
|
||
|
1.- Elige
valores de h
positivos y cada vez más pequeños y mira el valor de la
velocidad media en la parte superior. Anota tus
conclusiones y da un valor aproximado para la v. instantánea con especial atención al
signo de la velocidad y al
crecimiento de la función. 2.- Elige, si aún no lo has hecho, h=0 y mira el valor de la velocidad media. No puede hacer la división por cero. 3.- Elige valores de h negativos acercándose a 0. Confirma el valor que habías elegido para la v. instantánea al acercarte por la derecha. Observa el crecimiento y el signo de la velocidad. 4.- Repite las pruebas en a=-1 donde la función crece |
||
|
CONCLUSIONES: Si tomo valores h positivos, Q se aproxima a P por la derecha de la gráfica. No puede calcularse la velocidad instantánea tomando h=0 Si h tiene signo negativo, el punto Q se aproxima a P por la izquierda. Cuando la función es decreciente, la velocidad media es negativa. Cuando la función es creciente, la velocidad media es positiva |
||
| 2. VELOCIDAD INSTANTÁNEA | ||
|
Como habrás visto tenemos un problema al tomar h =0. Vamos a estudiar el punto P acercándonos a él. Fíjate en la siguiente escena, es igual que la anterior con un zoom para poder estudiar de cerca el punto x=a. El parámetro h tiene más cifras decimales y podemos estudiar puntos más próximos simulando el cálculo del límite.
|
||
1.- Elige valores de h cada vez más próximos a cero usando las flechas. 1.1.- Si te aproximas a P por la derecha (h>0) verás que la velocidad media va dando valores cada vez más próximos al nº -10 m/sg. En concreto fíjate en h=0.0001 1.2.- Si te aproximas a P por la izquierda (h<0) ocurre lo mismo, las velocidades se van aproximando al nº -10 m/sg. Fíjate ahora en h=-0.0001 1.3.- Observa el valor de la diferencia según te vas aproximando a h=0, especialmente en h=0.0001. 1.4.- Estima un valor para el límite cuando h tiende a cero |
||
|
Como hemos visto antes, en h=0 no podemos calcular la velocidad, pero parece razonable que, puestos a asignar una velocidad instantánea en a, y ya que la división por cero no permite calcularla, elijamos ese valor al que nos estamos acercando tanto por la izquierda como por la derecha. ¿Es el que habías elegido? Si no es así repite en otro valor de a. Se llama velocidad instantánea en a a ese nº y si recuerdas que la idea de aproximación o tendencia está recogida en la definición de límite entenderás que escribamos
|
||
| 3. LA PENDIENTE DE LA TANGENTE | ||
|
También te parecerá razonable que hablemos de la recta tangente a la curva en un punto P como el límite de las rectas secantes que pasan por P y Q cuando Q se aproxima a P.
En la siguiente escena puedes ver la evolución de las secantes al aproximarse Q a P
|
||
|
1.- Observa cómo varía
la pendiente de
la secante para algunos puntos Q que
se van aproximando a P por la derecha y después por la
izquierda. 2.- Fíjate en el valor que toma la pendiente de la recta tangente y compara con los valores que iban tomando las pendientes de las secantes. 3.-Elige otro punto P donde la función sea decreciente usando el ratón o la flecha de a. Observa de nuevo la evolución de las pendientes al acercarte a P por ambos lados y compara con la pendiente de la tangente |
||
Es fácil entender por qué decimos
que Pendiente de
secante PQ es 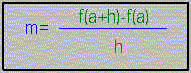
Pendiente de la
tangente a y=f(x) en x=a es |
||
| 4. TASA DE VARIACIÓN INSTANTÁNEA | ||
|
Ya te imaginarás que para comparar dos magnitudes cualesquiera en un punto, y no en un intervalo, vamos a necesitar introducir la idea de la tasa de variación instantánea:
|
||
|
||
| CONCLUSION
Para estudiar el ritmo de crecimiento de una función en un punto se utiliza la tasa de variación instantánea Dada una función y=f(x) hemos encontrado una forma de medir la tasa de variación instantánea en un punto P observando el límite de las tasas de variación media al aproximarnos a ese punto Si una función crece en un punto su TVI es positiva. Si una función decrece en un punto su TVI es negativa |
||
| 5. DERIVADA DE UNA FUNCIÓN EN UN PUNTO | ||
|
Para recoger todas estas ideas sobre el estudio de funciones que relacionan valores de x con valores de y , en concreto sobre su ritmo de crecimiento tenemos una herramienta: La derivada de una función y=f(x) en el punto de abscisa x= a es la pendiente de la tangente a la curva en el punto (a,f(a)) y coincide con la tasa de variación instantánea de la curva en el punto a.
|
||
|
1.- Da a h valores
positivos y negativos aproximándose a cero y el cero.
Estudia la escena. 2.- Busca puntos con derivada positiva y observa cómo crece la función al pasar por esos puntos 3.- Busca puntos con derivada negativa y observa cómo crece la función 4.- Busca puntos con derivada 0 y fíjate en la tangente. 5.- Limpia la escena, pon h=0 y recorre la gráfica dando distintos valores a a. Si te fijas en los puntos D verás que describen una gráfica nueva. Pon FUNCIÓN=1 y verás la gráfica completa. Se trata de la FUNCIÓN DERIVADA de la de la escena |
||
|
DEFINICION: La derivada de una función en un punto x=a es la pendiente de la tangente a la curva en ese punto y coincide con la tasa de variación instantánea de y respecto de x en ese punto. Su fórmula es
Si y=f(x) es derivable en algunos puntos de su dominio, podemos definir una función nueva que llamaremos y´ o f´ que a cada x le hace corresponder la derivada de f en x (esta es f´(x)). Esta función estará definida sólamente en los puntos en los que f es derivable.Ya que es una función también se suele escribir y=f´(x) |
||
| Rosa Jiménez Iraundegui | ||
 |
||
| © Ministerio de Educación y Ciencia. Año 2001 | ||