| SOLUCIONES
A LOS EJERCICIOS
PROPUESTOS
|
|
| 1.-
Efectúa las siguientes operaciones y simplifica el resultado:
Esta
escena te puede ayudar a hallar, al menos, resultados parciales de
sumas y restas. Más abajo hay otra escena con multiplicaciones y
divisiones
|
|
|
| a) (6-5i)+(2-i)-2(-5+6i)=18-18i |
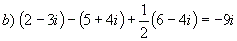 |
| c) (3+2i)(4-2i)=16+2i |
| d) (-i+1)(3-2i)(1+3i)=16-2i |
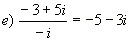 |
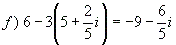 |
 |
|
|
VOLVER
|
|
| 2.-
Obtén polinomios cuyas raíces sean:
En esta escena se pueden
realizar multiplicaciones y divisiones de complejos
|
|
|
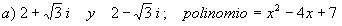 |
| b) -3i y 3i; polinomio= x2+9 |
| c) 1+2i y 3-4i; polinomio = x2+(-4+2i)x+(11+2i) |
d) ¿Cómo han de ser las
raíces para que los coeficientes del polinomio sean reales?
Han de ser complejos conjugados tal como ocurre en los apartados
a) y b) |
VOLVER
|
|
| 3.-
¿Cuánto debe valer x,
real, para que (25-x.i)2
sea imaginario puro?
Debe
ser x= 25.
Lo puedes comprobar en la escena anterior
VOLVER
|
|
| 4.-
Representa gráficamente z1=3+2i,
z2=2+5i, z1+z2.
Comprueba que z1+z2 es una diagonal
del paralelogramo de lados z1 y z2.
Lo
puedes comprobar en la primera escena de esta misma página.
VOLVER
|


