
 |
RAZONES TRIGONOMÉTRICAS Y OPERACIONES ENTRE ÁNGULOS |
| Geometría | |
| 1. RAZONES TRIGONOMÉTRICAS DEL ÁNGULO SUMA. | ||
|
En el siguiente gráfico utilizo letras griegas para nombrar los ángulos; es una notación habitual a la que debes acostumbrarte. Debemos tener presente que OQ=1 y que QS es perpendicular a OS. Los ángulos a son iguales porque sus lados son perpendiculares. En la ilustración figuran las demostraciones de dos fórmulas muy importantes. Observa que el seno de la suma no es la suma de los senos y que el coseno de la suma tampoco es la suma de los cosenos. |
||
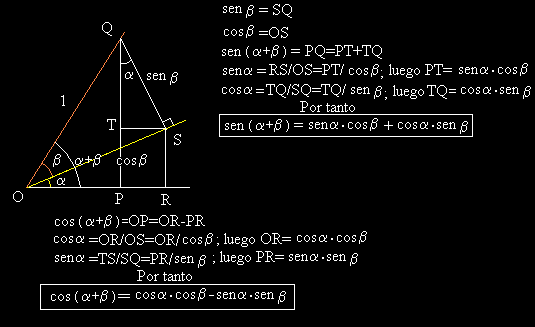
|
|
|
|
La siguientes escenas nos sirven para estudiar situaciones muy variadas. Por ejemplo: ¿Qué ocurre cuando los ángulos son iguales?. ¿Es el seno de 120º el doble del seno de 60º?. Prueba poniendo en la escena A=60º y B=60º. ¿Y si los ángulos se diferencian en 90º?.¿Y si es la suma la que vale 90º? Haz las mismas investigaciones con 180º. Compara los resultados con lo que ya has estudiado sobre estos ángulos. |
||
|
||
|
|
||
|
|
||
|
||
|
La tangente del ángulo suma se obtiene
mediante el siguiente proceso:
En resumen, las fórmulas del ángulo suma son:
|
||
| Jesús Fernández Martín de los Santos | ||
 |
||
| © Ministerio de Educación y Ciencia. Año 2001 | ||