|
Representar la función:
y=Öx2-1
|
|
1. INFORMACIÓN
EXTRAÍDA DE LA FUNCIÓN
|
|
|
1)
Dominio
-
x2-1<0
entre -1 y 1 luego la raíz
cuadrada no existe entre estos valores, por tanto la función
está definida en (-¥,-1]
È
[1,¥).
|
|
2) Cortes con los
ejes y signo
-
Con
el eje OY: cuando x=0 la
función no está definida luego no tiene corte con este eje.
Con
el eje OX: resolvemos la
ecuación x2-1=0
resultando las soluciones x=-1, y x=1 luego los puntos de corte son: (-1,0) y (1,0)
-
En
este caso f(x)>0 en todos los demás puntos del dominio.
|
|
Cambia
el valor de x en la escena o arrastra el
punto rojo con el ratón, podrás ver los valores que toma y=f(x). Observa
como en el intervalo (-1,1) la función no alcanza ningún valor. |
|
3) Simetría
|
|
|
4) Asíntotas
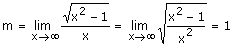
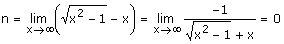
|
|
Comprueba
que cuando x®-¥
y®+¥
;
y que cuando
x®+¥
y®+¥,
y que además el valor de y
se aproxima más al de x (o a -x)
cuando mayor (o menor) es éste.
Utiliza el ZOOM para verlo mejor.
|
|

|


