
Idea intuitiva.
 |
Continuidad de funciones: Idea intuitiva. |
| 2º Bachillerato CNS y T. | |
| Estudio de las funciones y = sgn(x) e y = 1/x. | ||||
|
Observa la escena que tienes a continuación. El parámetro m puede tomar dos valores:1,2. Seleccionándolos puedes ver dos funciones diferentes. Si seleccionas m=1 verás representada la función y = sgn(x) :
La función anterior no está definida para x=0. Si seleccionas m=2 verás representada la función y = 1/x | ||||
Pon el valor del parámetro m igual a 1. La función es y = sgn(x) : 1.- Recorre la función arrastrando el punto amarillo con el ratón. ¿Qué ocurre en el punto 0?. En el parámetro B.x, toma valores cercanos a cero, tanto por la izquierda (menores que cero), como por la derecha (mayores que cero). Habrás visto que, al pasar por 0, el punto B da un salto, su ordenada pasa de (-1) a (1). 2.- Piensa: Esta función ¿es continua ó discontinua?. Razona tu respuesta.
| Pon ahora el valor del parámetro m igual a 2. La función es y = 1/x : 3.- Recorre la función arrastrando el punto amarillo del eje de abscisas con el ratón, ¿qué ocurre en el punto 0?. Varía el parámetro B.x para valores muy cercanos a 0, si B = (B.x, B.y), son las coordenadas del punto B de la gráfica, cuando la abscisa B.x está muy cercana a cero, tanto por la derecha como por la izquierda, ¿qué valores toman sus imágenes (B.y)?, ¿cuál es la imagen de B.x = 0?. 4.- ¿Cómo te parece esta función, continua ó discontinua?. Razona tu respuesta. | |||
Estudio de las funciones 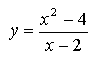 e e |
|||||||
|
Analizaremos, en primer lugar, la función | |||||||
5.- ¿Qué le pasa al punto B cuando B.x = 2?, ¿Cuál es su imagen?. ¿Cuál es la imagen de los puntos cercanos a 2, tanto a su derecha como a su izquierda? 6.-¿Piensas que esta función puede ser continua?. Razona tu respuesta.
|
Analizaremos, ahora, la función
|
|
7.-¿Qué ocurre para los valores B.x < -5 o B.x = -5? ¿Es continua?. Razona tu respuesta. | ||||
| Estudio de la función y = log(x). | |
|
Observa la función y = log (x), no existe para los x<0 o x=0, pero ¿cómo se comporta para los demás valores de x?. Vamos a estudiar su continuidad en un punto A, que tu puedes elegir sin más que variar el valor del parámetro A.x ,que es la abscisa de A. Una vez fijado A, con el punto P puedes recorrer la gráfica, arrastrándolo con el ratón, o cambiando los valores del parámetro P.x, que es la abscisa de P. | |
|
9.-¿Crees que esta función es continua en el punto A ? Razona tu respuesta. | |
| Belén Pérez Zurdo. | ||
 |
||
| © Ministerio de Educación y Ciencia. Año 2001 | ||