|
Cramer Gabriel (1704-1752)
 Matemático
Suizo. Sus contribuciones como diseminador de las ideas matemáticas le
ganaron un bien merecido lugar en la historia de las matemáticas. Cramer
viajó bastante y conoció a muchos de los grandes matemáticos de su época.
Estos contactos y amistades condujeron a una correspondencia abundante a
través de la cual se difundía la información sobre nuevos
descubrimientos matemáticos. Matemático
Suizo. Sus contribuciones como diseminador de las ideas matemáticas le
ganaron un bien merecido lugar en la historia de las matemáticas. Cramer
viajó bastante y conoció a muchos de los grandes matemáticos de su época.
Estos contactos y amistades condujeron a una correspondencia abundante a
través de la cual se difundía la información sobre nuevos
descubrimientos matemáticos.
El trabajo más conocido de Cramer, "Introduction á l'analyse des
lignes courbes algébriques" (1750), es un estudio y una clasificación
de curvas algebraicas; la regla de Cramer apareció en el apéndice.
Aunque la regla lleva su nombre, variantes de la idea básica fueron
planteadas antes por otros matemáticos. Sin embargo, la notación
superior de Cramer ayudó a aclarar y popularizar la técnica.
El exceso de trabajo, combinado con una caída de un carruaje, provocaron
su fallecimiento en 1752. Cramer era una persona de buen corazón y
agradable, nunca contrajo matrimonio. Sus intereses eran amplios. Escribió
sobre filosofía de las leyes y del gobierno, y sobre la historia de las
matemáticas. Trabajó en una oficina pública, participó en la artillería
y en actividades de fortificaciones para el gobierno, instruyó a
trabajadores sobre técnicas de reparación de catedrales y efectuó
excavaciones de archivos catedralicios. Cramer recibió numerosos honores
por sus actividades.
(Biografía
sacada de la pg http://ar.geocities.com/matematicamente/cramer.htm)
Sistemas
de Cramer
En
esta unidad didáctica estudiaremos los sistemas de ecuaciones lineales
con igual número de ecuaciones que de incógnitas:
Ejemplo:
3x+2y+4z=8
2x+2y+2z=6
-1x+4y+1z=9
|
equivale a |
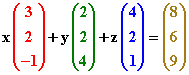 |
Dado un sistema
de igual número de ecuaciones que de incógnitas,
u1x+v1y+w1z=b1
u2x+v2y+w2z=b2
u3x+v3y+w3z=b3
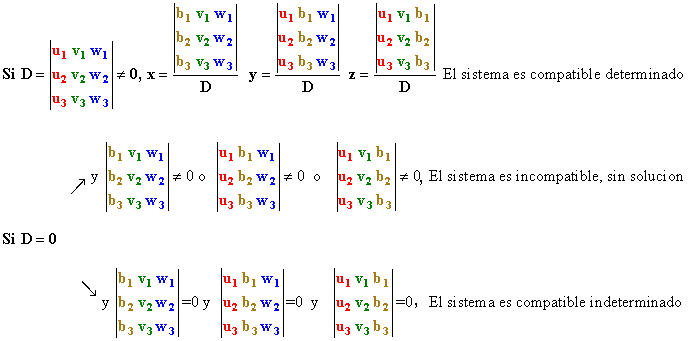
Es decir,

|


