
 |
Límites de funciones: Límite en un punto (idea intuitiva) I. |
| 2º de Bachillerato CCNN y Tecnológico. Análisis. | |
| Introducción. | |
|
Cuando se trabaja con funciones, frecuentemente nos interesa averiguar el comportamiento de una determinada función cuando la variable independiente, x, se aproxima a un determinado valor, a. En otras palabras: queremos averiguar si la función se aproxima a un determinado valor, b, aumenta indefinidamente, disminuye indefinidamente o no tiene un comportamiento claramente definido.
A continuación vamos a describir las distintas posibilidades de comportamiento de una función en las cercanías de un punto, indicando la notación habitual en Matemáticas para referirse a ellas.
| |
| Caso 1. | |
|
Los valores de la función f(x) se aproximan a un cierto número real, b, cuando la variable independiente se aproxima al punto a. | |
|
Acerca la x al valor de a en la imagen siguiente y comprueba cómo cuando x se acerca al punto a (línea blanca), f(x) se aproxima a b (línea verde). | |
|
Expresaremos este hecho mediante la siguiente expresión:
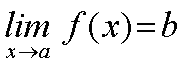
Y diremos que b es el límite de f(x) cuando x tiende al punto a. | |
| Caso 2. | |
|
Los valores de la función f(x) crecen indefinidamente cuando la variable independiente se aproxima al punto a. | |
|
Acerca la x al valor de a en la imagen siguiente y comprueba cómo cuando x se acerca al punto a (línea blanca), f(x) se hace tan grande como se quiera (línea verde). Desplaza hacia arriba la gráfica y cambia la escala si es preciso para visualizarlo mejor.
| |
|
Expresaremos este hecho mediante la siguiente expresión:
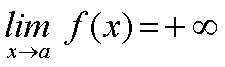
Y diremos que el límite de f(x) cuando x tiende al punto a es infinito. Diremos, además, que la recta x=a es una asíntota vertical de la función y=f(x). | |
|
OBSERVACIÓN: Decir que el límite es infinito no significa que "infinito" sea un número. Se trata simplemente de una manera sencilla de expresar el hecho de que la función no se acerca a ningún valor concreto, pero su comportamiento en las cercanías del punto a está perfectamente definido: toma valores tan grandes como se quiera. | |
| Caso 3. | |
|
Los valores de la función f(x) decrecen indefinidamente cuando la variable independiente se aproxima al punto a. | |
|
Acerca la x al valor de a en la imagen siguiente y comprueba cómo cuando x se acerca al punto a (línea blanca), f(x) se hace tan pequeña como se quiera (línea verde). Desplaza hacia abajo la gráfica y cambia la escala si es preciso para visualizarlo mejor.
| |
|
Expresaremos este hecho mediante la siguiente expresión:
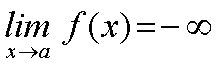
Y diremos que el límite de f(x) cuando x tiende al punto a es menos infinito. También en este caso diremos que la recta x=a es una asíntota vertical de la función y=f(x). | |
|
OBSERVACIÓN: Decir que el límite es menos infinito no significa que "menos infinito" sea un número. Se trata simplemente de una manera sencilla de expresar el hecho de que la función no se acerca a ningún valor concreto, pero su comportamiento en las cercanías del punto a está perfectamente definido: toma valores tan pequeños como se desee. | |
| Caso 4. | |
|
Los valores de la función f(x) ni se acercan a ningún valor concreto ni aumentan ni disminuyen indefinidamente cuando la variable independiente se aproxima al punto a. | |
|
Acerca la x al valor de a en la imagen siguiente y comprueba cómo cuando x se acerca al punto a (línea blanca), los valores de f(x) (línea verde) van oscilando sin acercarse a ningún valor concreto. Asimismo nunca sobrepasan ciertos valores, tanto por encima como por debajo. Amplía la escala lo necesario para observar con más detalle lo que sucede cerca del punto a.
| |
|
Expresaremos este hecho diciendo que la función f(x) no tiene límite en el punto a. | |
|
OBSERVACIÓN: El hecho de que digamos que en este caso no existe el límite no debe hacernos pensar que en los dos casos anteriores sí existe este límite pero que es infinito. En los casos anteriores tampoco existe el límite cuando x tiende al punto a. Sin embargo, debemos distinguir esas situaciones de la correspondiente al caso actual, pues en los casos anteriores, aunque no exista el límite, el comportamiento de la función alrededor del punto a está perfectamente determinado, cosa que no sucede ahora. Recordemos entonces que decir que el límite es infinito quiere decir que no hay límite, pero que la función crece (o decrece) continuamente al acercarse la x al punto a. | |
| José Luis Alonso Borrego | ||
 |
||
| © Ministerio de Educación y Ciencia. Año 2001 | ||