
Expresiones indeterminadas I.
 |
Propiedades de los límites: Expresiones indeterminadas I. |
| 2º de Bachillerato CCNN y Tecnológico. Análisis. | |
| Introducción. | |
|
En los capítulos anteriores hemos analizado el comportamiento de los límites finitos e infinitos en relación con las cuatro operaciones básicas: suma, resta, producto y cociente. A no ser que hayas sido poco observador, habrás notado que no hemos analizado todos los casos posibles. En concreto los casos que no hemos analizado son los siguientes:
La razón por la que no hemos analizado esos casos es muy simple: en esos cuatro casos no hay una pauta general, es decir, al calcular cualquiera de esos cuatro tipos de límites podemos obtener los resultados más dispares dependiendo de las funciones con las que trabajemos. Por eso decimos que estos límites son indeterminados.
|
| Indeterminaciones del tipo 0/0. | |
|
En toda esta página consideraremos dos funciones f(x) y g(x) con límite cero en un cierto punto a.
Es decir
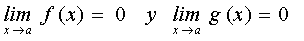
Vamos a comprobar con una serie de ejemplos que, en estas circunstancias, el límite cuando x tiende al punto a de f(x)/g(x) puede valer cualquier cosa: en unos casos valdrá +¥, en otros valdrá cualquier número positivo, en otros valdrá cero, en otros valdrá cualquier número negativo y en otros valdrá -¥. Incluso puede suceder que los límites laterales no coincidan. |
|
Haz que la x tome valores próximos al punto a, tanto por la izquierda como por la derecha y observa qué sucede con f(x)/g(x). En este ejemplo el límite cuando x tiende al punto a de f(x)/g(x) es más infinito. |
Haz que la x tome valores próximos al punto a, tanto por la izquierda como por la derecha y observa qué sucede con f(x)/g(x). En este ejemplo el límite cuando x tiende al punto a de f(x)/g(x) es menos infinito. |
|
Haz que la x tome valores próximos al punto a, tanto por la izquierda como por la derecha y observa qué sucede con f(x)/g(x). En este ejemplo el límite cuando x tiende al punto a de f(x)/g(x) es más infinito por la derecha y menos infinito por la izquierda. |
El parámetro t que aparece en esta gráfica permite que trabajemos con distintas funciones f(x). Todas ellas tienen límite cero en el punto a, pero el cociente entre f(x) y g(x) va cambiando. Selecciona un valor cualquiera para t, tanto positivo como negativo. Después, acerca la x al punto a para averiguar cuánto vale el límite del cociente cuando x tiende al punto a. Repite el ejercicio para distintos valores de t y observa que se puede obtener cualquier límite. |
|
Haz que la x tome valores próximos al punto a, tanto por la izquierda como por la derecha y observa qué sucede con f(x)/g(x). En este ejemplo el límite de f(x)/g(x) cuando x tiende al punto a es uno. |
Haz que la x tome valores próximos al punto a, tanto por la izquierda como por la derecha y observa qué sucede con f(x)/g(x). En este ejemplo el límite de f(x)/g(x) cuando x tiende al punto a es cero. |
|
Infinitésimos. | |
|
Se dice que una función, f(x), es un infinitésimo en un punto a si
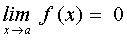
Todas las funciones que aparecen en los ejemplos anteriores son infinitésimos en el punto a. Desde el punto de vista intuitivo un infinitésimo es una función que se aproxima a cero tanto como queramos sin más que aproximar x al punto a. Una de las cuestiones más interesantes en el estudio de los infinitésimos es su comparación. Comparar dos infinitésimos nos permite averiguar cuál de los dos se acerca a cero más rápidamente y este conocimiento puede ser muy útil en otros cálculos. Asimismo el saber que dos funciones muy diferentes tienden a cero a la misma velocidad en las cercanías de un punto nos permite que bajo ciertas condiciones podamos sustituir una por otra en nuestros cálculos y de esa manera simplificarlos. El procedimiento para comparar dos infinitésimos en un punto a consiste en calcular el límite de su cociente cuando x tiende al punto a. Este procedimiento nos permite establecer la siguiente clasificación:
En todo lo que sigue supondremos que f(x) y g(x) son dos infinitésimos en un mismo punto a, es decir.
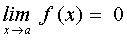 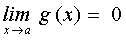
|
| José Luis Alonso Borrego | ||
 |
||
| © Ministerio de Educación y Ciencia. Año 2001 | ||