
 |
Propiedades de los límites: Propiedades fundamentales. |
| 2º de Bachillerato CCNN y Tecnológico. Análisis. | |
| Introducción. | |
|
En este capítulo vamos a estudiar algunas de las propiedades más importantes de los límites. Se trata de unas propiedades muy intuitivas pero de gran importancia para obtener resultados posteriores, en especial para determinar las propiedades de las funciones continuas.
| |
| Unicidad del límite. | |
|
"Si una función tiene límite en un punto, éste es único".
Dicho de otra manera, si existe el límite de f(x) cuando x se acerca a un cierto punto, a, f(x) no puede acercarse simultáneamente a dos puntos distintos, b y c.
|
|
Vamos a analizar la afirmación anterior a partir de la gráfica siguiente. Antes de llegar a ninguna conclusión errónea, observa que no se trata de la gráfica de una función.¿Sabrías explicar por qué?. A pesar de ello, esta gráfica nos ayudará a entender la propiedad que estamos estudiando. En lo que sigue vamos a suponer que la gráfica que aparece es la gráfica de una determinada función con dos límites distintos en el punto a, a los que denominaremos b y c, y vamos a comprobar que esa suposición nos lleva a una contradicción.
| |
|
1.- Fíjate sólo en la parte superior de la gráfica. Acerca la x al punto a. ¿Cuánto vale el límite de la función cuando x tiende al punto a?. | |
|
2.- Fíjate ahora sólo en la parte inferior de la gráfica. Acerca la x al punto a. ¿Cuánto vale el límite de la función cuando x tiende al punto a?. | |
|
3.- Observa ahora las parejas de líneas horizontales que aparecen en la gráfica. La pareja de líneas verdes representa un entorno del punto b y de radio e. Por su parte, la pareja de líneas azules representa un entorno del punto c, también de radio e. Como ves, inicialmente estos entornos se solapan. ¿Es posible conseguir un valor de e para el cual esos dos entornos no tengan ningún punto en común? Si la respuesta es afirmativa encuentra sobre la gráfica alguno de esos valores. | |
|
4.- De nuevo fíjate sólo en la parte superior de la gráfica. Con el valor de e que has obtenido en la cuestión anterior, averigua a qué distancia máxima, d, puede estar la x de a para que la distancia entre f(x) y b sea menor que e con toda seguridad | |
|
5.- Contesta a la misma cuestión anterior, pero fijándote sólo en la parte inferior de la gráfica. | |
|
Ahora que has encontrado las respuestas a las cuestiones anteriores, vamos a analizarlas. Si has contestado bien a la primera pregunta habrás llegado a la conclusión de que 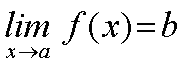
Por otra parte, si has contestado correctamente a la segunda cuestión habrás obtenido que 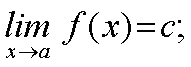
Es decir, hipotéticamente, nos encontramos con una función que tiene dos límites diferentes en el punto a. Ahora bien, el hecho de que b sea el límite de la función f(x) en el punto a significa que fijado un número positivo, e, es posible encontrar otro número positivo, d, tal que si x dista de a menos que d, entonces f(x) dista de b menos que e. | |
|
Ejercicio.
Si los puntos b y c hubiesen estado mucho más próximos entre sí, la respuesta a la tercera cuestión ¿seguiría siendo afirmativa? Razona la respuesta.
| |
| Acotación. | |
|
"Si una función tiene límite en un punto, existe un entorno de ese punto en el que la función está acotada".
En otras palabras, en los alrededores del punto a, la gráfica de la función está totalmente contenida en una franja limitada por dos rectas horizontales.
|
|
Contesta a las cuestiones que se te plantean referentes a la gráfica siguiente: | |
|
1.- ¿Está acotada la función de la imagen? Razona la respuesta. | |
|
2.- Selecciona el valor de e que quieras. Una vez seleccionado, averigua para qué valor de d se cumple que si x está entre las dos líneas azules verticales, entonces f(x) está entre las dos líneas verdes horizontales con toda seguridad. | |
|
3.- Selecciona otro valor diferente de e y repite la operación anterior. ¿Es siempre posible encontrar un valor de d que cumpla que si x está entre las dos líneas azules verticales, entonces f(x) está entre las dos líneas verdes horizontales con toda seguridad? | |
|
En la imagen anterior está claro que se cumple 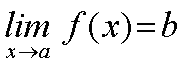
por lo que la respuesta a la tercera cuestión planteada debe ser forzosamente afirmativa.
| |
| Conservación del signo. | |
|
"Si el límite de una función en un punto no es cero, existe un entorno de ese punto en el que la función tiene el mismo signo que el límite".
Dicho de otra forma, si el límite en el punto a es un número positivo, existe un entorno de a en el que la función es positiva; pero si el límite es negativo, existirá un entorno de a en el que la función será negativa. Si el límite es cero puede que no sea cierta ninguna de ambas cosas, aunque como veremos con algunos ejemplos pueden darse también en este caso ambas situaciones.
|
|
Contesta a las cuestiones que se te plantean referentes a la gráfica siguiente: | |
|
1.- Pulsa el botón inicio de la gráfica anterior. Como puedes ver, inicialmente la franja contenida entre las dos líneas verdes horizontales tiene una parte por encima del eje de abscisas y otra parte por debajo de este eje. Busca algún valor de e para el que esa franja esté totalmente por encima del eje de abscisas. | |
|
2.- Con el valor de e obtenido en la cuestión anterior seleccionado, averigua para qué valor de d se cumple que si x está entre las dos líneas azules verticales, entonces f(x) está entre las dos líneas verdes horizontales con toda seguridad. Aumenta la escala si fuera preciso para verlo con mayor claridad. | |
|
3.- Desplaza ahora la x al interior de la franja limitada por las dos rectas verticales azules. ¿Qué puedes afirmar del signo de f(x) siempre que x esté dentro de esa franja? | |
|
4.- El parámetro u de la gráfica sirve para trabajar con una función similar a la anterior, pero con un límite diferente en el punto a. Cambia el valor de u hasta que consigas que el valor de b sea 0.10. Ampliando mucho la escala si es preciso para ver mejor, repite con esta nueva gráfica las tres cuestiones anteriores. | |
|
5.- ¿Sería posible repetir este proceso con cualquier valor de b positivo, aunque fuera muy muy pequeño? | |
|
6.- Modifica el valor de u para que los valores de b sean iguales a -1 y a -0.1 y contesta de nuevo a todas las cuestiones anteriores. En estos casos el valor de e tiene que ser tal que la franja limitada por las líneas verdes horizontales esté completamente por debajo del eje de abscisas. | |
|
7.- Cambia el valor de u hasta conseguir que b valga 0 ¿Qué sucede en este caso para cualquier valor de e? | |
|
El resultado de las cuestiones anteriores nos indica que si b>0 (respectivamente b < 0) entonces es posible encontrar un valor de e, de forma que b-e > 0 (respectivamente b+e < 0) y como b es el límite de f(x) cuando x tiende al punto a, resulta que para ese valor de e existe otro valor, d, tal que si x Î (a-d,a+d), entonces f(x) Î (b-e,b+e) y, por lo tanto, si x está en ese entorno de a, f(x) es positivo (respectivamente negativo). | |
|
Ejercicio. En el caso de que b=0, en el ejemplo anterior sucede que en los puntos cercanos al punto a por la izquierda la función toma valores positivos, pero en los cercanos por la derecha la función toma valores negativos. Sin embargo, ésta no es siempre así. En los siguientes ejemplos vamos a comprobar cómo pueden presentarse situaciones con b=0, en las que en cierto entorno de a, f(x) es siempre positiva, o siempre negativa. | |
|
Haz variar x entre las dos líneas verticales azules y comprueba que f(x) siempre toma valores positivos, tanto a la izquierda como a la derecha de a. Amplia la escala si es preciso para verlo con más claridad. |
Haz variar x entre las dos líneas verticales azules y comprueba que f(x) siempre toma valores negativos, tanto a la izquierda como a la derecha de a. Amplia la escala si es preciso para verlo con más claridad. |
| Monotonía. | |
|
"Sean h, f y g tres funciones definidas en un entorno reducido de un punto a, y tales que en ese entorno se verifica h(x) £ f(x) £ g(x). Si existen los límites de h(x) y de g(x) cuando x tiende al punto a y ambos límites coinciden, por ejemplo en b, entonces también tiene que existir el límite de f(x) cuando x tiende al punto a y ese límite es necesariamente b.". |
|
En la imagen, las funciones h(x) y g(x) tienen gráficas de color amarillo. Evidentemente para ambas funciones se cumple que su límite en el punto a es b. En color rojo tenemos la gráfica de f(x). Como puede verse, se tiene h(x) £ f(x) £ g(x) para todo x alrededor del punto a. Cada vez que modifiques algo en la gráfica la función f cambiará pero manteniendo sus propiedades. De esta forma podremos ver que cualquier el resultado que se afirma es cierto sea cual sea la función f(x) siempre y cuando cumpla las condiciones establecidas.
| |
|
1.- Pulsa el botón inicio de la gráfica anterior. Las líneas azules horizontales representan un entorno del punto b de radio e y las líneas azules verticales representan un entorno del punto a de radio d. | |
|
2.- Con el valor actual de e, averigua cuál es el valor máximo de d para el que se cumple que si x está en el interior del entorno de a de radio d, tanto g(x) como h(x) están en el interior del entorno de b de radio e. Aumenta la escala si es preciso para verlo con más detalle. ¿Qué sucede con los valores de f(x) cuando x está en ese mismo entorno? | |
|
3.- Dale a e varios valores más pequeños y contesta para cada uno de esos valores a la misma cuestión anterior. ¿Es siempre posible encontrar un valor de d que cumpla lo que se afirma en esa cuestión? | |
|
Si has encontrado la respuesta correcta a las cuestiones planteadas te habrás dado cuenta de que para cualquier valor de e siempre es posible encontrar un valor d tal que si |x-a| < d entonces |f(x)-b| < e. En otras palabras:
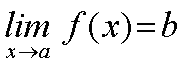
| |
| José Luis Alonso Borrego | ||
 |
||
| © Ministerio de Educación y Ciencia. Año 2001 | ||