

Presentación Objetivos Contenidos Requisitos Introducción Proyecto Evaluación
Actividades Guiadas
En las siguientes actividades se propone el análisis de las escenas de las aplicaciones disponibles y se muestran algunos ejemplos.
§§§ Abre la página unidades didácticas.htm con el navegador, elige alguno de los ejemplos que presenta y revisa cómo se han confeccionado las escena.
No es necesario hacerlo con una página concreta, pero para que se vean dos ejemplos se muestran a continuación el análisis de Coordenadas cartesianas.htm y Función seno.htm.
§§§ Abre la página Coordenadas cartesianas.htm con el navegador.
§§§ Abre el editor de páginas html para escribir tus comentarios del análisis de algunas actividades e intercalar, si lo deseas, las escenas que quieras.
§§§ Observa la primera escena (Organización del plano) y escribe lo que te sugiere, respecto a la finalidad de esa actividad, las características de su configuración y las sugerencias que te parezcan útiles, por ejemplo:
Finalidad: Parece que la finalidad de esta escena es que los alumnos observen el plano como una retícula donde se destacan los ejes y el origen de coordenadas.
Recursos: Para conseguirlo se han suprimido casi todos los botones del entorno y se utiliza como recurso de interacción la pulsación del botón izquierdo para que comiencen a asociar los puntos del plano con los pares de números y la retícula.
Destaca: Lo más llamativo de esta escena es que no se usa ninguna herramienta de interacción (CONTROL) y, a pesar de ello, la hay.
Sugerencia: Para destacar los ejes y el origen podrían utilizarse colores que fueran más llamativos y suprimir también el botón Créditos.
§§§ Observa la segunda escena (El plano cartesiano) y escribe lo que te sugiere, respecto a la finalidad de esa actividad, las características de su configuración y las sugerencias que te parezcan útiles, por ejemplo:
Finalidad: En este caso se pretende que el alumnos sean conscientes de que el sistema de representación elegido sirve para que se pueda asignar una pareja de números a todos los puntos del plano.
Recursos: Se utilizan sólo los controles estándar: la escala para el zoom, Ox y Oy para el movimiento de ejes, así como sus nombres, también se muestran los números de la escala en los ejes para que sirvan de referencia.
Destaca: Destaca el buen efecto de zoom que se consigue con un incremento variable, relativo a la propia escala, si el incremento fuera fijo en unos momentos el zoom sería excesivamente lento y en otros demasiado rápido.
Sugerencia: El campo decimales de la escala se puede suprimir ya que no se muestra el valor de la escala. Para mejorar el efecto de desplazamiento de los ejes se puede disminuir el incremento. También pueden asignarse colores distintos a los ejes, mediante una recta y=0.
§§§ Analiza el resto de las escenas de la página Coordenadas cartesianas.htm.
§§§ Analiza la primera escena de la Función seno (Definición de seno de un ángulo agudo) y escribe lo que te sugiere, respecto a la finalidad de esa actividad, las características de su configuración y las sugerencias que te parezcan útiles, por ejemplo:
Finalidad: Se pretende que los alumnos recuerden la definición del seno de un ángulo agudo y que puedan comprobar, gráficamente y numéricamente los valores del seno para distintos ángulos.
Elementos: Esta configuración es compleja ya que intervienen bastantes elementos: los fundamentales son los que figuran como controles numéricos: el ángulo alfa y el lado AB. En AUXILIARES se define el punto A y se calculan el resto son valores: los puntos B y C, los segmentos BC y AC.
Recursos: Se utilizan los CONTROLES el segmento AB y el ángulo alfa, que se le denomina A. Para representar los arcos de los ángulos A y B se usa la herramienta ARCO, el primero con centro en A dependiendo de alfa y el segundo fijo, ya que es recto, con centro en B. Con TEXTO se escriben, con distintos colores, los valores de los segmentos y del seno. Se usa SEGMENTO para representar los vértices y los lados del triángulo.
Destaca: Lo más llamativo de esta escena es como la escritura de las fracciones con TEXTO. También destaca la utilización de ARCO para definir un ángulo fijo y otro variable.
Sugerencia: Par ver que el seno es independiente de la posición del triángulo que se use, se puede poner el punto A como control y los puntos B y C dependientes de A. De esta forma moviendo A se traslada todo el triángulo.
§§§ Analiza la cuarta escena de la Función seno (La función seno) y escribe lo que te sugiere, respecto a la finalidad de esa actividad, las características de su configuración y las sugerencias que te parezcan útiles, por ejemplo:
Finalidad: Se pretende que los alumnos vean una construcción de la función seno asociándola con la definición.
Elementos: Esta configuración es muy compleja ya que intervienen numerosos elementos: el principal es el ángulo alfa, que figura como parámetro, y las gráficas del seno de la circunferencia goniométrica. Otros elementos son los puntos que se representan sobre el eje de abscisas, sobre la curva del seno y sobre la circunferencia goniométrica, para cada valor de alfa. Por último, el texto fijo que aparece debajo de la circunferencia, los arcos, los segmentos y los valores que representan el ángulo en grados, el ángulo en radianes y el valor seno.
Recursos: Se utilizan casi todas las herramientas para conseguir los diferentes efectos.
- En la CONFIGURACIÓN Se define un tamaño de escena WIDTH de 500 puntos para que se vea bien la gráfica en el intervalo (0;6,28).
- En ESPACIO Se resaltan los EJES, se difumina la RED y ocultan los TEXTOS, y se ocultan los botones el CONFIG y LIMPIAR que no hay que usarlos.
- En CONTROLES se define la escala y el eje Ox para que se vea la parte del plano que interesa, pero evita que se puedan cambiar y se usa el ángulo alfa del que depende la interacción.
- En AUXILIARES calcula las coordenadas de los puntos sobre la gráfica del seno (P) y sobre la circunferencia (A) que luego se representarán
- En GRÁFICOS:
- ECUACIÓN se usa para representar la circunferencia goniométrica difuminada.
- CURVA se utiliza para representar la tenue función seno y la porción de gráfica entre cero y alfa en naranja.
- SEGMENTO se usa para representar los segmentos correspondientes a la abscisa y al valor del seno, tanto sobre la gráfica de la función seno, como sobre la circunferencia goniométrica.
- PUNTO se usan para representar los puntos correspondientes a cada ángulo sobre la gráfica del seno y sobre la circunferencia goniométrica.
- ARCO sirve para representar el ángulo alfa sobre la circunferencia goniométrica.
- TEXTO escribe "Circunferencia goniométrica", el nombre de la función, el ángulo en grados y radianes y el valor del seno para cada ángulo.
Destaca: Lo más llamativo de esta escena es la adaptación del tamaño de la escena y del ESPACIO a lo que requiere la gráfica del seno. También la utilización de CURVA para dibujar la gráfica del seno dos veces, primero en el intervalo (0;6,28) y luego en (0,alfa), así como el empleo de fondo en la primera de estas representaciones y en la de ECUACIÓN, que representa la circunferencia usando la función implícita correspondiente. (Si se quita la orden fondo se puede observar que la representación es muy lenta). Por último, es llamativa la utilización de coordenadas variables, dependiendo de las variables de ESPACIO, para representar los textos, para conseguir que éstos se muevan cuando se desplazan los ejes, aunque en este caso no tiene ningún efecto y podrían ponerse fijas.
§§§ Después de haber analizado cuatro o cinco escenas crea una nueva página con tu nombre y apellidos.htm y guarda en ella comentarios que te parezcan más apropiados.
En las siguientes actividades vas a modificar la cuarta actividad de la Función seno, con la que se ha trabajado en las actividades anteriores, para que la representación se realice para cualquier valor de la abscisa, en todo su dominio, de forma que los textos relativos a la circunferencia permanezcan junto a ella, pero los de la función "se muevan" al mover los ejes.
§§§ Abre la página Unidades didácticas.htm con el navegador y accede a la cuarta escena de la Función seno (La función seno).
En primer lugar debes permitir que la escala pueda cambiar y que se pueda desplazar el gráfico horizontalmente.
§§§ En CONTROLES asigna a la escala mínimo 10 y máximo 60, en Ox y en alfa suprime los límites mínimo y máximo, para que puedan tomar cualquier valor. Prueba el efecto y modifica los incrementos.
§§§ En ESPACIO elimina los botones config y limpiar y desactiva red, que no se usa y escribe los nombres de los ejes.
§§§ En GRÁFICOS suprime las tres instrucciones de TEXTO que escriben los nombres de los ejes y del origen de coordenadas, ya que no hacen falta.
Ahora hay que modificar las ecuaciones que representan las gráficas para que lo hagan en todo el plano visible.
§§§ Suprime la primera línea de CURVA y añade la ECUACIÓN que represente la función seno y=sen(x) con color 505050, que no sea visible y activa el fondo.
Para que las expresiones correspondientes al nombre y valor de la función y al ángulo en radianes, sean fijos en la escena, aunque se muevan los ejes, hay que hacer que no dependan de Ox, por lo tanto hay que sustituir Ox por su valor inicial que es -128. Tampoco deben depender de Oy ya que su valor no cambia.
§§§ En GRÁFICOS cambia las líneas de TEXTO en las que aparezca Ox u Oy, Ox por el valor fijo´-128 y Oy por 0, excepto en los dos últimos para que el nombre de circunferencia gonométrica aparezca siempre junto a la circunferencia, cambia la ordenada de estas dos últimas líneas para que el texto no quede sobre la circunferencia.
§§§ Comprueba que con estos cambios se producen los efectos que se buscaban y guarda la actividad y la escena en el archivo nombre y apellidos.htm que has creado en esta práctica.
§§§ Elige alguna otra escena de la misma página o de otra, añádela a la página anterior con una explicación de lo que pretendes y de cómo lo haces.
A continuación se va a crear una nueva actividad para la página Punto-pendiente_2.htm de la carpeta Ejercicios, con la que se ha trabajado en las prácticas anteriores.
En esta nueva actividad se trata de relacionar la pendiente de una recta con la tangente del ángulo de esa recta. Para ello queremos representar dos rectas paralelas, sobre una de ellas se debe mostrar el ángulo que forma la recta con el eje OX y en la otra que aparezcan como segmentos la abscisa y ordenada de cada punto para mostrar que el cociente de la ordenada y la abscisa es la tangente del ángulo y la pendiente de la recta.
§§§ Abre la página Punto-pendiente_2.htm con el navegador y con el editor.
§§§ Copia la sexta actividad y pégala a continuación como séptima. Ponle el título "Pendiente de una recta y la tangente del ángulo que forma con OX".
§§§ Explica que la tangente de un ángulo de una recta que pasa por el origen es el cociente entre la ordenada y la abscisa de cualquier punto de esa recta que sea distinto del origen.
§§§ Define la escena con las siguientes características:
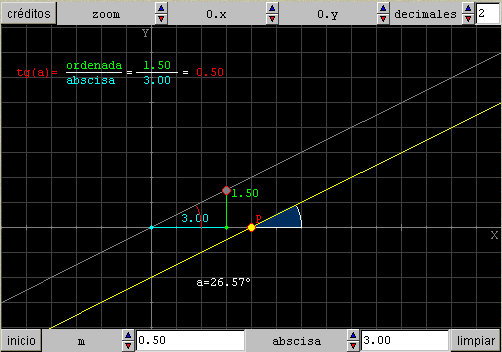
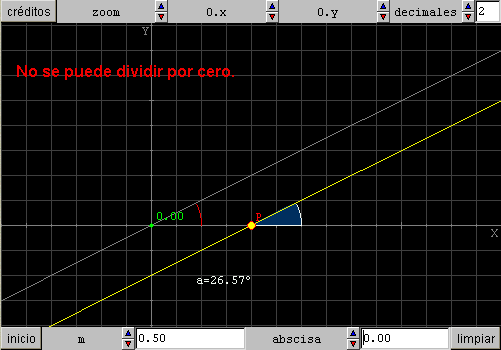
Cuando el control C es el origen de coordenadas debe escribirse no se puede dividir por cero, en lugar de las expresiones de la tangente.
§§§ Escribe alguna propuesta de trabajo para que el alumno vea la relación entre el valor de la pendiente y el ángulo.
§§§ Crea alguna otra actividad relacionada con las anteriores, por ejemplo la ecuación de la recta que pasa por dos puntos.
§§§ Guarda el archivo Punto-pendiente_2.htm modificado.
Presentación Objetivos Contenidos Requisitos Introducción Proyecto Evaluación
| Juan Madrigal Muga | ||
 |
||
| © Ministerio de Educación y Ciencia. Año 2001 | ||