| 12.
La proporción bidimensional, tridimensional y
d-dimensional |
| Observación: La razón o
proporcionalidad que hemos considerado hasta
ahora no es más que un modelo bidimensional
(comparamos dos dimensiones, dos medidas). Actividad 12.1
Modelo del canon bidimensional.
- Observa
las fotografías siguientes y, ya como
experto, establece un orden de belleza.
- Halla
el canón de belleza de cada una de ellas
¿qué observas? (compruébalo).
|
 |
 |
 |
| |
|
|

|

|

|
| |
|
|
Actividad
12.2 Modelos o canones alternativos,
tridimensional, d-dimensional.
- ¿Qué
te sugiere el resultado que has obtenido
anteriormente?
- ¿Introducimos
una tercera medida? ¿Cual?
- ¿Como
las relacionamos? ¿Cual sería el
número áureo tridimensional? ¿Cual
sería el ortoedro áureo?
- ¿Es
suficiente o necesitaremos más medidas?
- Busca
algunas referencias y documentos en la
red que te ayuden, por ejemplo ("the
plastic number", "Van der
Laan", "Le Corbusier" o
"Padovan")
|
|
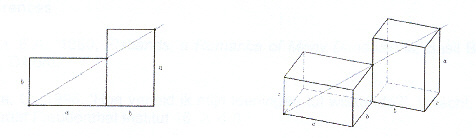
Observación:
Aquí
tienes una primera ayuda:
- En
la figura de la izquierda podemos
observar una propiedad que verifica un
rectángulo áureo "horizontal"
y su correspondiente
"vertical".
- En
la figura de la derecha se representa una
extensión tridimensional de lo que
podríamos definir como ortoedro áureo.
|
|
|
|
| Actividad
12.3 La investigación matemática. Creo
que has podido constatar que las Matemáticas
pueden ayudar a modelar la naturaleza, a
comprender nuestra realidad concreta cotidiana y
nuestra innata abstracción, a dar una
explicación racional de nuestro entorno.
Pero
el estudio, el análisis, la reflexión, la
lógica, ... te permitirán llegar a más.
¡Estás invitado!
|
|
|


