MESOPOTAMIA
BloqueHistoria
 
1. CIVILIZACIÓN BABILÓNICA.
Ésta es una civilización que se desarrolló entre los ríos Tigris y Eufrates desde finales del cuarto milenio antes de Cristo y hasta la caída de la ciudad de Babilonia en manos de los persas en el 538 aC. Sus habitantes, los sumerios, idearon el primer sistema de escritura (escritura cuneiforme) que ha llegado a nosotros en miles de tablillas de cerámica halladas en las excavaciones arqueológicas de Uruk . Es una escritura que al menos tiene 5000 años de antigüedad. En el tercer milenio antes de Cristo los acadios invadieron estas tierras, adoptaron su escritura y desarrollaron un sistema de numeración posicional; es decir, el valor de una cifra depende de la posición que ocupa dentro del número. La base de su sistema era el número 60 y conservamos su uso en las medidas de tiempo y de ángulos. En la tabla puedes ver las aportaciones de los babilonios al desarrollo de las Matemáticas.
Escritura cuneiforme

 

 Derecha: Tablilla con escritura precuneiforme. Parece hecha con un estilete cilíndrico.

Izquierda: ejemplo de escritura cuneiforme. El estilete utilizado es un prisma triangular.
Teoría de números

 
Álgebra
  • Ecuaciones lineales
  • Sistemas de ecuaciones lineales
  • Ecuaciones de segundo grado
  • Algunas ecuaciones cúbicas

 
Geometría
  • Áreas de figuras planas
  • Volumen del tronco de cono o de la pirámide
  • Triángulos rectángulos
  • La altura de un triángulo isósceles divide a la base en dos partes iguales
  • Obtención del apotema a partir de la cuerda y el radio de la circunferencia

 

2.ESCRITURA CUNEIFORME Tablilla Plimpton 322 de la Universidad de Columbia: incluye listas de

 números de interpretación 

variada

(1900 a 1600aC)
Los babilonios nos han dejado muestras de su escritura en muchas tablillas de barro, como la de la foto. Mediante una herramienta con forma de prisma triangular dejaban marcas en forma de cuña en la arcilla blanda. Posteriormente la tablilla se dejaba secar al sol o se cocía en hornos. Dependiendo de la posición del prisma se obtenían marcas diferentes y, combinándolas en distintas posiciones, daban origen a palabras o números.

 Este material ha resistido muy bien el paso del tiempo y miles de tablillas se han ido encontrando en las distintas excavaciones arqueológicas. A finales del siglo XIX se localiza una crónica de guerra escrita en tres lenguas, persa, elamita y babilonio que permitirá empezar a traducir esta escritura.  Sin embargo, hasta el siglo XX y gracias a Thureau en Francia y a Neugebauer en Alemania y Estados Unidos, no se descifra el significado de las de contenido matemático. 

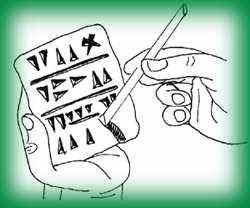
Arriba: Ilustración de la mano del 

escriba tallando una tablilla con una caña

3. TEORÍA DE NÚMEROS     

Derecha: un número en notación sexagesimal.
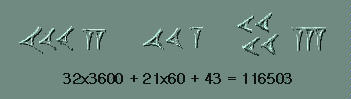Antes del 1.700 aC los babilonios idearon un sistema de numeración posicional (las cifras valen según su posición dentro del número) y sexagesimal (en base 60 cada unidad grande está formada por 60 unidades más pequeñas). El sistema utiliza dos signos básicos, la unidad , una  cuña en posición vertical, y la decena , una cuña en posición horizontal. Combinando éstas adecuadamente, escriben los 59 primeros números. No utilizaron el cero hasta el 400 aC, utilizando dos cuñas oblícuas. Como ejemplo puedes ver el 59. Si el número es mayor que 60, como 116.503 del que puedes ver su escritura en la ilustración superior, obtenían mediante divisiones sucesivas entre 60 los restos de cada división. El número lo escribían con esos restos.
116503 60  
  565 1941 60
   250   141 32
     103     21  
      43 116503=32·602+21·60+43
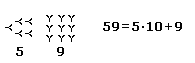
Los babilonios usaban este mismo sistema para representar las fracciones sexagesimales, es decir con potencias de 60 en el denominador. Cumplían la misma función que nuestras unidades decimales y así manejaban expresiones como 2·60-1+3·60-2 En una de las tablillas de la colección Yale, que data del periodo babilónico antiguo, se incluye el cálculo de la raíz cuadrada de 2 con tres cifras "decimales" sexagesimales. Con nuestros dígitos se escribe 1;24,51,10 y equivale a 1+24/60+51/3600+10/216000=1.4144028, es decir las tres primeras cifras decimales son exactas.
Para el cálculo de la raíz cuadrada de un número "a" ingeniaron un proceso que se repite indefinidamente y consiste en:

Se elige una primera aproximación a1.

A partir de ella se obtiene una segunda aproximación hallando la media aritmética de a1 y el cociente a/a1=b1, es decir a2=(a1+b1)/2 y es una aproximación mejor.  

Se trata de un algoritmo iterativo que puede prolongarse indefinidamente. En cada etapa el valor obtenido mejora al anterior.

Sin embargo, los babilonios, o al menos sus escribas, eran muy aficionados a confeccionar tablas con los valores que debían utilizar. De ellos nos han llegado tablas de multiplicar, de inversos, de cuadrados y cubos, de raíces cuadradas y cúbicas, de potencias sucesivas de un número... 
Para la división utilizaban la multiplicación por el inverso.
Entre las listas de números halladas aparecen unas ternas que se ajustan a las fórmulas p2-q2, 2pq y p2+q2 . Estas ternas permiten construir triángulos rectángulos con distintos números y encontraron 38 pares siendo p menor que 60 (ternas pitagóricas ). En la tablilla 322 aparecen las 15 primeras.
Hay constancia de la existencia de tablas con las potencias sucesivas de algunos números, por ej de 9-16-1;40 y 3;45 ( 9, 16, 100, y 225 con numeración decimal). Para los números que no son cuadrados perfectos utilizaban la interpolación lineal con la que estaban muy familiarizados. Así, hay constancia de un problema en el que se pide el tiempo que tardará en doblarse un capital con un interés del 20% anual. La respuesta es 3;47,13,20 años y puede obtenerse de esta forma:

Nosotros usamos la fórmula C=Co·(1+r)t y diríamos 2=1·(1+20/100)t y por tanto 2=1'2t. Para hallar t usamos los logaritmos y decimos t=log 2/log 1'2=3'801784. Ten en cuenta que t es el exponente al que hay que elevar 1'2 para obtener 2 como resultado (definición de logaritmo de 2 en base 1'2).

En Mesopotamia  (1+20/100) corresponde al número cuneiforme 1;12. Se trata de hallar el exponente al que hay que elevar este número para obtener 2 como resultado. Buscamos dos potencias, una mayor y otra menor que 2, y serán (1;12)3 = 1;43,40 y (1;12)4=2;4,25. Mediante una regla de tres el escriba obtiene el número 3;47,13,20 años, es decir 3'787. Nosotros tomaríamos con los logaritmos de nuestras calculadoras 3'802. 

En la siguiente escena puedes ver una representación gráfica del problema de la interpolación lineal

La solución se obtiene gráficamente buscando el punto que está en el segmento PQ y en la ordenada  deseada,  tal y como se estudia hoy. Los datos se muestran en la tabla inferior. Se incluyen los números en notación sexagesimal. Puedes resolver el problema para otros datos cambiando los puntos P y Q y triplicando o multiplicando por otro número el capital depositado

t 3 ? 4 7 ? 8
 C(t)=1'2t 1'728 2   2'0736 3'583 4 4'2998
   sexagesi 1;43,40 ? 2;4,25 ? ? ?
 t=3'787=3;47,13,20
Pulsando sobre la escena con el botón derecho del ratón aparece un menú que te permite modificar los datos. Los puntos P y Q puedes cambiarlos arrastrando con el ratón. Utiliza el cambio de escala o mueve los ejes cuando lo necesites. Puedes activar la animación o pararla pulsando Pausa o Anima.
5. GEOMETRÍA
 Los babilonios utilizaban para calcular áreas y volúmenes muchas fórmulas más o menos exactas. Para calcular el área del cuadrilátero hacían el producto de las medias aritméticas de los pares de lados opuestos. El volumen del tronco de cono o pirámide lo hallaban tomando el producto de la altura por la media aritmética de las áreas de las bases. Para el tronco de pirámide utilizaban también una fórmula que es correcta:

Ya hemos hablado del uso del teorema de Pitágoras en las tablillas Plimpton. En la colección hallada en Susa aparecen resultados en los que se manejan semejanzas de figuras.
1.- En la escena puedes ver el círculo de radio 6 y los perímetros de los polígonos inscritos. Los babilonios calculaban el área del círculo multiplicando el cuadrado del radio por 3 ()
Pulsando sobre la escena con el botón derecho del ratón aparece un menú que te permite cambiar el nº de lados. Usa los pulsadores de colores que hay junto al zoom y junto a los ejes OX y OY si te hace falta.

2.-En la tabla aparecen unos datos que pertenecen a las tablillas halladas en Susa, a 300 km de Babilonia, en notación sexagesimal

Razón de las áreas y los cuadrados de los lados
polígono razón
pentágono 1;40
hexágono 2;37,30
heptágono 3;41
Razón del perímetro del hexágono regular y la circunferencia circunscrita
razón=0;57,36
Compara las razones de los babilónicos con las actuales y verás su grado de aproximación Esto da una aproximación

4. ÁLGEBRA
Los babilonios manejaban con soltura los cálculos algebraicos.

 Eran capaces de resolver cualquier ecuación de segundo grado que tuviera soluciones positivas y esto hace 4.000 años. Hay que tener en cuenta que hasta la edad moderna no se contemplan soluciones negativas. Hasta esa época estas ecuaciones se clasifican en tres tipos y ellos ya sabían resolverlas todas mediante transformaciones como multiplicar la ecuación por un número. Estos cálculos aparecen dentro de problemas como: halla el lado de un cuadrado si su área menos el lado es igual a 14;30. La solución que figura es:

" Toma la mitad de 1, que es 0;30, y multiplica 0;30 por 0;30, que es 0;15; suma este número a 14;30, lo que da 14,30;15; éste es el cuadrado de 29;30; ahora suma 0;30 a 29;30, cuyo resultado es 30, que es el lado del cuadrado"

Para hallar la raíz de 14,30;15 usan sus tablas de cuadrados o de raíces. 

Si la ecuación era del tipo ax2+bx=c, la resolvían multiplicando por "a" para convertirla en (ax)2+b(ax)=c y hallando "ax" en primer lugar. Este es el primer ejemplo de sustitución de la incógnita para resolver ecuaciones y un gran hallazgo para los primitivos babilónicos.

Una de las tablas de uso más frecuente en el álgebra babilónica es la de los valores de n3+n2  siendo "n"un número natural. Utilizaban estas tablas para resolver ecuaciones cúbicas del tipo x3+x2=a . Si en la ecuación aparecían coeficientes distintos de 1 la transformaban para completar el cubo y sustituían la incógnita igual que en las de 2º grado. Así, para la ecuación ax3+bx2=c multiplicaban por a2/b y hallaban ax/b.

El uso de la sustitución de la incógnita les permitió resolver algunas ecuaciones de 4º o 8º grado, las que hoy llamamos bicuadradas.
Puedes cambiar los valores de p y q desplegando el menú y obtener todas las ternas que cumplen

                    

En la tabla 322 de la foto superior aparecen ordenadas en columnas unas listas de números que parecen ajustarse a los posibles lados de triángulos rectángulos (ternas pitagóricas) y elementos de esos triángulos. Los números que figuran se ajustan a las fórmulas 

Las filas están ordenadas en sentido decreciente según la expresión a/b, para nosotros la razón trigonométrica secante de C; la primera columna de la izquierda está formada por números que coinciden con sec2 A empezando con sec2 45º y terminando en sec2 31º. Sin embargo, no existe nada parecido a la medida de ángulos que se utiliza hoy y es más probable que siguieran criterios basados en proporcionalidad de segmentos. 

Parece razonable suponer que las utilizaran para construir triángulos rectángulos de formas variadas. 

Utiliza el cambio de escala o mueve los ejes cuando lo necesites.
       
           
  Rosa Jiménez Iraundegui
 
© Ministerio de Educación y Ciencia. Año 2001