
 |
CON LAS CIFRAS 1, 2, ..., 9 |
| Bloque. Taller de Matemáticas | |
| SUMAS Y TORRE | |
 En el libro Nuevos Pasatiempos Matemáticos de Martin Gardner figura el siguiente:
En el libro Nuevos Pasatiempos Matemáticos de Martin Gardner figura el siguiente:
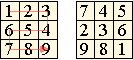
"Hay muchas formas de disponer las cifras 1, 2, ..., 9 en cuadro de 3x3 para que representen una suma; por ejemplo, como se puede ver en la figura, 745+236=981. Hay igualmente muchos modos de disponer los nueve dígitos en un cuadro de 3x3 de manera que una torre de ajedrez los pueda recorrer en forma creciente y siguiendo una trayectoria continua, uno de estos se puede ver en la figura. El problema consiste en reunir en un único cuadro de 3x3 las dos características, es decir, en formar con los nueve dígitos una matriz cuadrada de tres por tres, que una torre pueda recorrer de forma continua pasando de cada dígito a su siguiente, de 1 a 9, y en la que la tercera fila sea la suma de las otras dos. La solución es única." La escena siguiente nos servirá para solucionar este problema sin tener que utilizar lápiz y papel, sencillamente, pinchando y arrastrando. |
|
|
Si sólo pensamos en hacer sumas con los dígitos 1, ..., 9, podemos obtener
hasta un máximo de 336 soluciones diferentes. Ahora bien, una vez obtenida una solución
es muy fácil obtener otras, ¿cómo? Sencillamente, intercambiando entre sí
los dos primeros números de una misma columa. Por lo tanto, a partir de una solución
podemos obtener otras 8, la ya conocida y otras 7 más.
Además, fijémonos en la solución propuesta 745+236=981, y observar que también vale 457+362=819, pues 45+36=81 y 7+2=9. Pues bien, esto ocurre con todas las soluciones; luego de una solución se pueden obtener 15 soluciones más. Así pues, las 336 soluciones las tenemos agrupadas en 21 grupos de 16 soluciones cada grupo (21·16=336). Cada vez que consigamos una solución, el mensaje "OK SUMA" nos aparecerá, y si además la torre puede hacer su camino, otro mensaje se mostrará. |
|
| RESTAS Y SUMAS | |
| En el próximo juego hay que colocar los números del 1 al 9 en las posiciones adecuadas, restarlos dos a dos según están unidos y sumar estos resultados. Objetivo: conseguir obtener el menor y el mayor valor de esta suma. | |
| Salvador Calvo-Fernández Pérez | ||
 |
||
| © Ministerio de Educación y Ciencia. Año 2003 | ||